The application of Newton's second law to the motion of a particle of a fixed mass,  , and acted upon by a force ,
, and acted upon by a force , 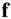 , gives the following important relationship – called the kinetics – for the determination of the particle's acceleration:
, gives the following important relationship – called the kinetics – for the determination of the particle's acceleration:
(2.22) 
The linear momentum ,  , of the particle is defined as the product of its mass,
, of the particle is defined as the product of its mass,  , and velocity,
, and velocity,  :
:
(2.23) 
Since the particle's mass is constant, the second law of motion given by Eq. (2.22) can alternatively be expressed as follows:
(2.24) 
which gives rise to the principle of linear momentum conservation if no force is applied to the particle.
The angular momentum ,  , of the particle about a point, o , is defined to be the vector product of the radius vector,
, of the particle about a point, o , is defined to be the vector product of the radius vector,  , of the particle from o and its linear momentum,
, of the particle from o and its linear momentum,  :
:
(2.25) 
By virtue of Eq. (2.24), it is evident that the angular momentum of the particle about o can vary with time, if and only if a torque , defined by  , acts on the particle about o :
, acts on the particle about o :
(2.26) 
This results in the principle of angular momentum conservation if no torque acts on the particle about o .
The work done on a particle by a force while moving from point A to point B is defined by the following integral of the scalar product of the force,  , and the particle's displacement,
, and the particle's displacement,  :
:
(2.27) 
The application of Newton's second law for the constant mass particle, Eq. (2.22), results in the following expression for the work done:
(2.28) 
where  and
and  are the speeds of the particle at the points A and B , respectively. Thus the net work done on a particle equals the net change in its kinetic energy ,
are the speeds of the particle at the points A and B , respectively. Thus the net work done on a particle equals the net change in its kinetic energy ,  .
.
Gravity, being the predominant force in space flight, must be understood before constructing any model for space flight dynamics. Consider two particles of masses,  and
and  , whose instantaneous positions in an inertial frame, OXYZ , are denoted by the vectors,
, whose instantaneous positions in an inertial frame, OXYZ , are denoted by the vectors,  and
and 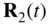 , respectively. The relative position of mass,
, respectively. The relative position of mass,  , with respect to the mass,
, with respect to the mass, 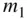 , is given by the vector
, is given by the vector  . By Newton's law of gravitation, the two particles apply an equal and opposite attractive force on each other, which is directly proportional to the product of the two masses, and inversely proportional to the distance,
. By Newton's law of gravitation, the two particles apply an equal and opposite attractive force on each other, which is directly proportional to the product of the two masses, and inversely proportional to the distance,  , between them. The equations of motion of the two particles are expressed as follows by Newton's second law of motion:
, between them. The equations of motion of the two particles are expressed as follows by Newton's second law of motion:
(2.29) 
(2.30) 
 being the universal gravitational constant . Adding the two equations of motion yields the important result that the centre of mass of the two particles is non‐accelerating:
being the universal gravitational constant . Adding the two equations of motion yields the important result that the centre of mass of the two particles is non‐accelerating:
Читать дальше

 , and acted upon by a force ,
, and acted upon by a force , 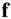 , gives the following important relationship – called the kinetics – for the determination of the particle's acceleration:
, gives the following important relationship – called the kinetics – for the determination of the particle's acceleration:
 , of the particle is defined as the product of its mass,
, of the particle is defined as the product of its mass,  , and velocity,
, and velocity,  :
:

 , of the particle about a point, o , is defined to be the vector product of the radius vector,
, of the particle about a point, o , is defined to be the vector product of the radius vector,  , of the particle from o and its linear momentum,
, of the particle from o and its linear momentum,  :
:
 , acts on the particle about o :
, acts on the particle about o :
 , and the particle's displacement,
, and the particle's displacement,  :
:

 and
and  are the speeds of the particle at the points A and B , respectively. Thus the net work done on a particle equals the net change in its kinetic energy ,
are the speeds of the particle at the points A and B , respectively. Thus the net work done on a particle equals the net change in its kinetic energy ,  .
. and
and  , whose instantaneous positions in an inertial frame, OXYZ , are denoted by the vectors,
, whose instantaneous positions in an inertial frame, OXYZ , are denoted by the vectors,  and
and 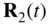 , respectively. The relative position of mass,
, respectively. The relative position of mass,  , with respect to the mass,
, with respect to the mass, 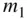 , is given by the vector
, is given by the vector  . By Newton's law of gravitation, the two particles apply an equal and opposite attractive force on each other, which is directly proportional to the product of the two masses, and inversely proportional to the distance,
. By Newton's law of gravitation, the two particles apply an equal and opposite attractive force on each other, which is directly proportional to the product of the two masses, and inversely proportional to the distance,  , between them. The equations of motion of the two particles are expressed as follows by Newton's second law of motion:
, between them. The equations of motion of the two particles are expressed as follows by Newton's second law of motion:

 being the universal gravitational constant . Adding the two equations of motion yields the important result that the centre of mass of the two particles is non‐accelerating:
being the universal gravitational constant . Adding the two equations of motion yields the important result that the centre of mass of the two particles is non‐accelerating:










