1 ...8 9 10 12 13 14 ...25 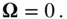
The net velocity of the point, P , is defined to be the time derivative of the radius vector, 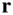 , which is expressed as follows according to the chain rule of vector differentiation:
, which is expressed as follows according to the chain rule of vector differentiation:
(2.6) 
and consists of the radial velocity component, 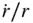 , and the circumferential velocity component,
, and the circumferential velocity component, 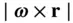 . Similarly, when the chain rule is applied to the velocity,
. Similarly, when the chain rule is applied to the velocity, 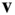 , the result is the net acceleration of the moving point, P , which is defined to be the time derivative of
, the result is the net acceleration of the moving point, P , which is defined to be the time derivative of 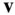 , or the second time derivative of
, or the second time derivative of 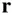 . In this special case of the radius vector,
. In this special case of the radius vector, 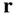 , always lying on a fixed plane, its angular velocity vector,
, always lying on a fixed plane, its angular velocity vector, 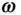 , is always perpendicular to the given plane (hence the direction
, is always perpendicular to the given plane (hence the direction 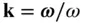 is constant), but can have a time‐varying magnitude,
is constant), but can have a time‐varying magnitude, 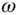 . Hence, Eq. (2.4)yields the following expression for the time derivative of
. Hence, Eq. (2.4)yields the following expression for the time derivative of 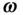 :
:
(2.7) 
When these results are substituted into Eq. (2.3), the following expression for the acceleration of the point, P , is obtained:
(2.8) 
The net acceleration of the point, P , parallel to the instantaneous radius vector, 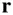 , is identified from Eq. (2.8)to be the following:
, is identified from Eq. (2.8)to be the following:
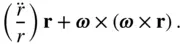
The direction of the term 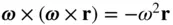 is always towards the instantaneous centre of rotation (i.e., along
is always towards the instantaneous centre of rotation (i.e., along 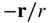 ). The other radial acceleration term,
). The other radial acceleration term, 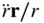 , is caused by the instantaneous change in the radius,
, is caused by the instantaneous change in the radius, 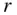 , and is positive in the direction of the increasing radius (i.e., away from the instantaneous centre of rotation).
, and is positive in the direction of the increasing radius (i.e., away from the instantaneous centre of rotation).
The component of acceleration along the vector  in Eq. (2.8)is perpendicular to both
in Eq. (2.8)is perpendicular to both 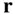 and
and 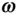 , and is given by
, and is given by
In terms of the polar coordinates ,  , we have
, we have  ; hence the motion is resolved in two mutually perpendicular directions, (
; hence the motion is resolved in two mutually perpendicular directions, (  ), where
), where 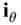 is a unit vector along the direction of increasing
is a unit vector along the direction of increasing 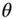 (called the circumferential direction ), defined by
(called the circumferential direction ), defined by
(2.9) 
Thus the rotating frame, 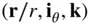 , constitutes a right‐handed triad. In this rotating coordinate frame, the motion of the point, P , is represented as follows:
, constitutes a right‐handed triad. In this rotating coordinate frame, the motion of the point, P , is represented as follows:
(2.10) 
(2.11) 
(2.12) 
(2.13) 
It is clear from Eq. (2.13)that in the rotating coordinate system, 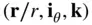 , the acceleration along the instantaneous radius vector,
, the acceleration along the instantaneous radius vector, 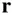 , is given by
, is given by
Читать дальше

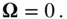
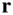 , which is expressed as follows according to the chain rule of vector differentiation:
, which is expressed as follows according to the chain rule of vector differentiation:
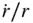 , and the circumferential velocity component,
, and the circumferential velocity component, 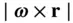 . Similarly, when the chain rule is applied to the velocity,
. Similarly, when the chain rule is applied to the velocity, 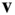 , the result is the net acceleration of the moving point, P , which is defined to be the time derivative of
, the result is the net acceleration of the moving point, P , which is defined to be the time derivative of 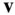 , or the second time derivative of
, or the second time derivative of 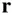 . In this special case of the radius vector,
. In this special case of the radius vector, 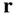 , always lying on a fixed plane, its angular velocity vector,
, always lying on a fixed plane, its angular velocity vector, 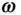 , is always perpendicular to the given plane (hence the direction
, is always perpendicular to the given plane (hence the direction 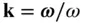 is constant), but can have a time‐varying magnitude,
is constant), but can have a time‐varying magnitude, 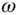 . Hence, Eq. (2.4)yields the following expression for the time derivative of
. Hence, Eq. (2.4)yields the following expression for the time derivative of 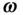 :
:

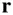 , is identified from Eq. (2.8)to be the following:
, is identified from Eq. (2.8)to be the following: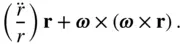
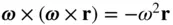 is always towards the instantaneous centre of rotation (i.e., along
is always towards the instantaneous centre of rotation (i.e., along 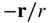 ). The other radial acceleration term,
). The other radial acceleration term, 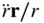 , is caused by the instantaneous change in the radius,
, is caused by the instantaneous change in the radius, 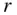 , and is positive in the direction of the increasing radius (i.e., away from the instantaneous centre of rotation).
, and is positive in the direction of the increasing radius (i.e., away from the instantaneous centre of rotation). in Eq. (2.8)is perpendicular to both
in Eq. (2.8)is perpendicular to both 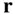 and
and 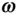 , and is given by
, and is given by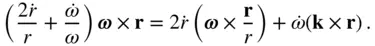
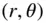 , we have
, we have 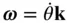 ; hence the motion is resolved in two mutually perpendicular directions, (
; hence the motion is resolved in two mutually perpendicular directions, ( 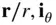 ), where
), where 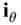 is a unit vector along the direction of increasing
is a unit vector along the direction of increasing 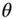 (called the circumferential direction ), defined by
(called the circumferential direction ), defined by
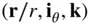 , constitutes a right‐handed triad. In this rotating coordinate frame, the motion of the point, P , is represented as follows:
, constitutes a right‐handed triad. In this rotating coordinate frame, the motion of the point, P , is represented as follows:



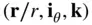 , the acceleration along the instantaneous radius vector,
, the acceleration along the instantaneous radius vector,  , is given by
, is given by










