1 ...7 8 9 11 12 13 ...25 (2.1) 
All the variables representing the motion of a spacecraft are changing with time , 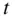 . The overdots represent the time derivatives, e.g.,
. The overdots represent the time derivatives, e.g., 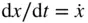 ,
, 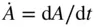 ,
, 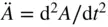 . The time derivative of a vector
. The time derivative of a vector 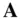 , which is changing both in its magnitude and its direction, requires an explanation.
, which is changing both in its magnitude and its direction, requires an explanation.
The time derivative of a vector, 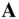 , which is changing both in magnitude and direction can be resolved in two mutually perpendicular directions – one along the original direction of
, which is changing both in magnitude and direction can be resolved in two mutually perpendicular directions – one along the original direction of 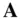 , and the other normal to it on the plane of the rotation of
, and the other normal to it on the plane of the rotation of 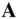 . The instantaneous angular velocity ,
. The instantaneous angular velocity , 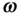 , of
, of 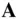 denotes the vector rate of change in the direction, whereas
denotes the vector rate of change in the direction, whereas 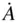 is the rate of change in its magnitude. By definition,
is the rate of change in its magnitude. By definition, 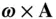 is normal to the direction of the unit vector,
is normal to the direction of the unit vector, 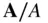 , and lies in the instantaneous plane of rotation normal to
, and lies in the instantaneous plane of rotation normal to 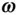 . The rotation of
. The rotation of 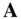 is indicated by the right‐hand rule , where the thumb points along
is indicated by the right‐hand rule , where the thumb points along 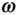 , and the curled fingers show the instantaneous direction of rotation, 1
, and the curled fingers show the instantaneous direction of rotation, 1 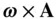 . The time derivative of
. The time derivative of 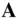 is therefore expressed as follows:
is therefore expressed as follows:
(2.2) 
where the term 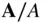 represents a unit vector in the original direction of
represents a unit vector in the original direction of 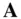 , and
, and 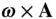 is the change normal to
is the change normal to 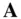 caused by its rotation. Equation ( 2.2) will be referred to as the chain rule of vector differentiation in this book.
caused by its rotation. Equation ( 2.2) will be referred to as the chain rule of vector differentiation in this book.
Similarly, the second time derivative of 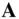 is given by the application of the chain rule to differentiate
is given by the application of the chain rule to differentiate 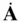 as follows:
as follows:
(2.3) 
Applying Eq. (2.1)to the time derivative of the angular velocity, 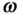 , we have the following expression for the angular acceleration of
, we have the following expression for the angular acceleration of 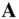 :
:
(2.4) 
where 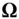 is the instantaneous angular velocity at which the vector
is the instantaneous angular velocity at which the vector 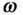 is changing its direction. Hence, the second time derivative of
is changing its direction. Hence, the second time derivative of 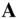 is expressed as follows:
is expressed as follows:
(2.5) 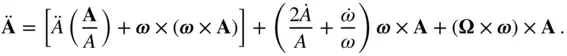
The bracketed term on the right‐hand side of Eq. (2.5)is parallel to 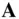 , while the second term on the right‐hand side is perpendicular to both
, while the second term on the right‐hand side is perpendicular to both 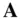 and
and 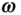 . The last term on the right‐hand side of Eq. (2.5)denotes the effect of a time‐varying axis of rotation of
. The last term on the right‐hand side of Eq. (2.5)denotes the effect of a time‐varying axis of rotation of 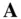 .
.
As a special case, consider the motion of a point, P , in a fixed plane described by the radius vector, 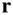 , which is changing in time. The vector
, which is changing in time. The vector 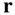 is drawn from a fixed point, o , on the plane, to the moving point, P , and hence denotes the instantaneous radius of the moving point from o . The instantaneous rotation of the vector
is drawn from a fixed point, o , on the plane, to the moving point, P , and hence denotes the instantaneous radius of the moving point from o . The instantaneous rotation of the vector 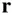 is described by the angular velocity,
is described by the angular velocity, 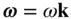 , which is fixed in the direction given by the unit vector
, which is fixed in the direction given by the unit vector 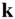 , normal to the plane of motion. Thus we have the following in Eq. (2.4):
, normal to the plane of motion. Thus we have the following in Eq. (2.4):
Читать дальше


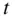 . The overdots represent the time derivatives, e.g.,
. The overdots represent the time derivatives, e.g., 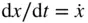 ,
, 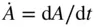 ,
, 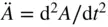 . The time derivative of a vector
. The time derivative of a vector 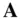 , which is changing both in its magnitude and its direction, requires an explanation.
, which is changing both in its magnitude and its direction, requires an explanation.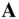 , which is changing both in magnitude and direction can be resolved in two mutually perpendicular directions – one along the original direction of
, which is changing both in magnitude and direction can be resolved in two mutually perpendicular directions – one along the original direction of 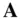 , and the other normal to it on the plane of the rotation of
, and the other normal to it on the plane of the rotation of 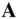 . The instantaneous angular velocity ,
. The instantaneous angular velocity , 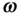 , of
, of 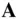 denotes the vector rate of change in the direction, whereas
denotes the vector rate of change in the direction, whereas 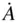 is the rate of change in its magnitude. By definition,
is the rate of change in its magnitude. By definition, 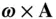 is normal to the direction of the unit vector,
is normal to the direction of the unit vector, 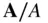 , and lies in the instantaneous plane of rotation normal to
, and lies in the instantaneous plane of rotation normal to 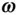 . The rotation of
. The rotation of 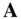 is indicated by the right‐hand rule , where the thumb points along
is indicated by the right‐hand rule , where the thumb points along 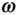 , and the curled fingers show the instantaneous direction of rotation, 1
, and the curled fingers show the instantaneous direction of rotation, 1 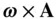 . The time derivative of
. The time derivative of 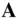 is therefore expressed as follows:
is therefore expressed as follows:
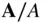 represents a unit vector in the original direction of
represents a unit vector in the original direction of 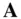 , and
, and 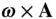 is the change normal to
is the change normal to 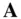 caused by its rotation. Equation ( 2.2) will be referred to as the chain rule of vector differentiation in this book.
caused by its rotation. Equation ( 2.2) will be referred to as the chain rule of vector differentiation in this book.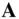 is given by the application of the chain rule to differentiate
is given by the application of the chain rule to differentiate 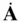 as follows:
as follows:
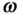 , we have the following expression for the angular acceleration of
, we have the following expression for the angular acceleration of 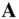 :
:
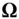 is the instantaneous angular velocity at which the vector
is the instantaneous angular velocity at which the vector 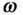 is changing its direction. Hence, the second time derivative of
is changing its direction. Hence, the second time derivative of 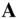 is expressed as follows:
is expressed as follows: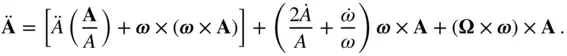
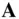 , while the second term on the right‐hand side is perpendicular to both
, while the second term on the right‐hand side is perpendicular to both 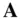 and
and 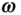 . The last term on the right‐hand side of Eq. (2.5)denotes the effect of a time‐varying axis of rotation of
. The last term on the right‐hand side of Eq. (2.5)denotes the effect of a time‐varying axis of rotation of 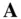 .
.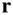 , which is changing in time. The vector
, which is changing in time. The vector 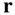 is drawn from a fixed point, o , on the plane, to the moving point, P , and hence denotes the instantaneous radius of the moving point from o . The instantaneous rotation of the vector
is drawn from a fixed point, o , on the plane, to the moving point, P , and hence denotes the instantaneous radius of the moving point from o . The instantaneous rotation of the vector 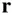 is described by the angular velocity,
is described by the angular velocity, 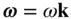 , which is fixed in the direction given by the unit vector
, which is fixed in the direction given by the unit vector 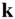 , normal to the plane of motion. Thus we have the following in Eq. (2.4):
, normal to the plane of motion. Thus we have the following in Eq. (2.4):










