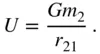(2.31) 
where
(2.32) 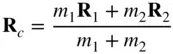
is the position of the centre of mass. This approach can be extended to a system of 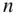 particles, where the
particles, where the 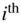 particle has the following equation of motion:
particle has the following equation of motion:
(2.33) 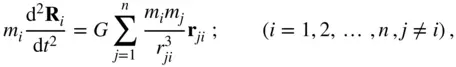
where 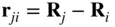 locates the
locates the 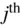 particle from the i thparticle (Fig. 2.2). A summation of Eq. (2.33)for all the particles produces the following result:
particle from the i thparticle (Fig. 2.2). A summation of Eq. (2.33)for all the particles produces the following result:
(2.34) 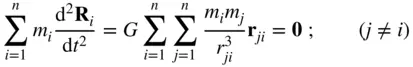
because 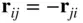 . Thus Eq. (2.31)is seen to be valid for the
. Thus Eq. (2.31)is seen to be valid for the 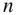 ‐particles problem, where the centre of mass is located by
‐particles problem, where the centre of mass is located by
(2.35) 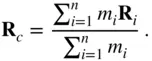
The non‐accelerating centre of mass is the result of the law of conservation of linear momentum in the absence of a net external force on the system of particles. Integrated twice with time, Eq. (2.31)shows that the centre of mass moves in a straight line at a constant velocity:
(2.36) 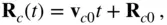
where 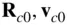 are constants (the initial position and the constant velocity, respectively, of the centre of mass).
are constants (the initial position and the constant velocity, respectively, of the centre of mass).
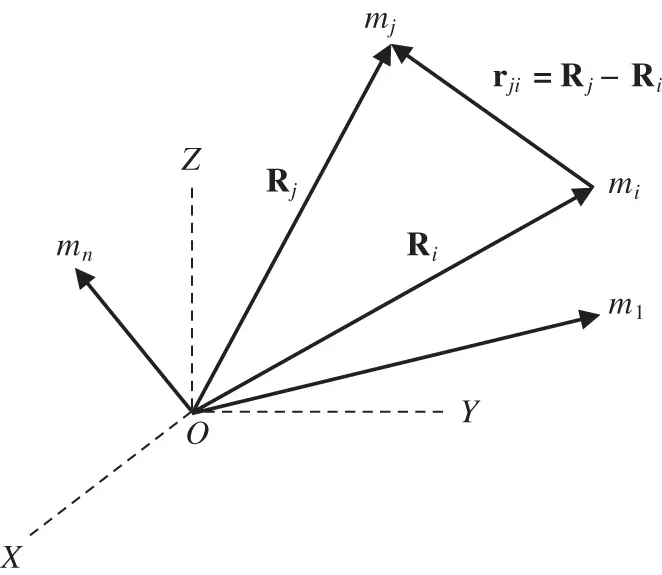
Figure 2.2A system of 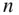 particles in an inertial reference frame OXYZ .
particles in an inertial reference frame OXYZ .
For the convenience of notation, consider the overdot to denote the time derivative relative to the inertial reference frame. Taking a scalar product of Eq. (2.33)with 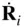 , and summing over all particles, we have
, and summing over all particles, we have
(2.37) 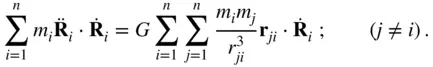
The term on the left‐hand side of Eq. (2.37)is identified to be the time derivative of the net kinetic energy of the system given by
(2.38) 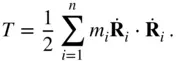
Before proceeding further, it is necessary to consider that gravity is a conservative force, because, as will be seen later, it has no influence on the net energy, 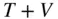 , of a system. A force which depends only upon the relative position of the masses (as gravity does) is a conservative force, and can be expressed as the gradient of a scalar function, called the gravitational potential . The gradient of a scalar, U , with respect to a position vector,
, of a system. A force which depends only upon the relative position of the masses (as gravity does) is a conservative force, and can be expressed as the gradient of a scalar function, called the gravitational potential . The gradient of a scalar, U , with respect to a position vector, 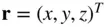 , is defined to be the following derivative of the scalar with respect to the given vector,
, is defined to be the following derivative of the scalar with respect to the given vector,
(2.39) 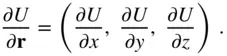
Thus, the gradient of a scalar with respect to a column vector is a row vector.
Consider, for example, an isolated pair of masses, 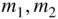 . The gravitational attraction on
. The gravitational attraction on 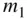 due to
due to 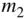 is given by the force,
is given by the force, 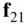 . By Newton's law of gravitation, we have
. By Newton's law of gravitation, we have
(2.40) 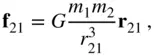
where the relative position of mass 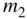 from the mass
from the mass 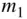 is given by the vector
is given by the vector 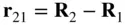 . Let
. Let 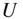 be the gravitational potential at the location of the particle,
be the gravitational potential at the location of the particle, 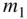 , defined by
, defined by
(2.41) 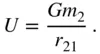
Читать дальше

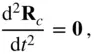
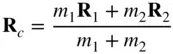
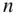 particles, where the
particles, where the 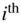 particle has the following equation of motion:
particle has the following equation of motion: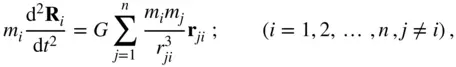
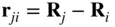 locates the
locates the 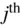 particle from the i thparticle (Fig. 2.2). A summation of Eq. (2.33)for all the particles produces the following result:
particle from the i thparticle (Fig. 2.2). A summation of Eq. (2.33)for all the particles produces the following result: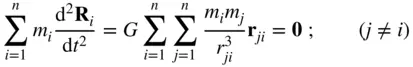
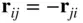 . Thus Eq. (2.31)is seen to be valid for the
. Thus Eq. (2.31)is seen to be valid for the 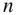 ‐particles problem, where the centre of mass is located by
‐particles problem, where the centre of mass is located by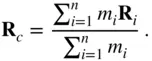
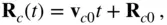
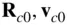 are constants (the initial position and the constant velocity, respectively, of the centre of mass).
are constants (the initial position and the constant velocity, respectively, of the centre of mass).
 particles in an inertial reference frame OXYZ .
particles in an inertial reference frame OXYZ .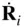 , and summing over all particles, we have
, and summing over all particles, we have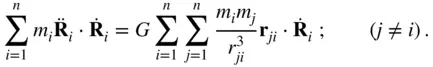
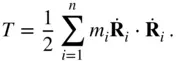
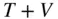 , of a system. A force which depends only upon the relative position of the masses (as gravity does) is a conservative force, and can be expressed as the gradient of a scalar function, called the gravitational potential . The gradient of a scalar, U , with respect to a position vector,
, of a system. A force which depends only upon the relative position of the masses (as gravity does) is a conservative force, and can be expressed as the gradient of a scalar function, called the gravitational potential . The gradient of a scalar, U , with respect to a position vector, 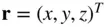 , is defined to be the following derivative of the scalar with respect to the given vector,
, is defined to be the following derivative of the scalar with respect to the given vector,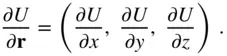
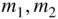 . The gravitational attraction on
. The gravitational attraction on 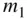 due to
due to 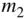 is given by the force,
is given by the force, 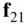 . By Newton's law of gravitation, we have
. By Newton's law of gravitation, we have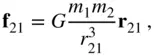
 from the mass
from the mass  is given by the vector
is given by the vector 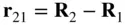 . Let
. Let 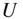 be the gravitational potential at the location of the particle,
be the gravitational potential at the location of the particle, 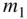 , defined by
, defined by