Ashish Tewari - Foundations of Space Dynamics

From Fig. 2.4it follows that

(2.76)

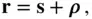
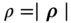and is a constant, because the attracting body is assumed to be a rigid body. When the position vectors 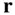and 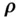are resolved in the Cartesian coordinates, we have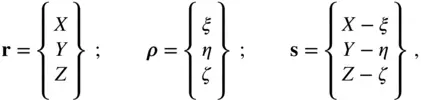

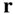(2.77)

the gravitational potential of the mass distribution is given by

(2.78)

and the gravitational acceleration at from the centre of mass of the attracting body is the following: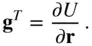

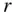(2.79)

To carry out the integration in Eq. (2.78), it is assumed that the body is entirely contained within the radius measured from its centre of mass; that is, 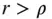for all points on the body. It is then convenient to expand the integrand in the following series: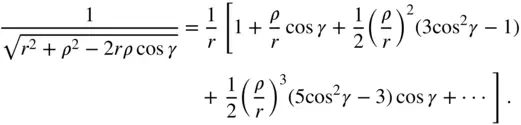

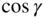(2.80)

Equation ( 2.80) is an infinite series expansion in polynomials of , and is commonly expressed as follows: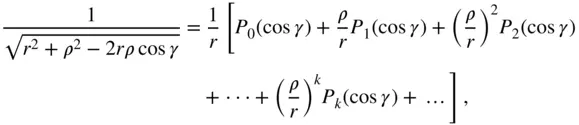

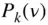(2.81)

where is the Legendre polynomial of degree k , defined by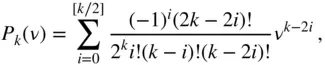

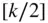(2.82)

with denoting the largest integer value of 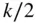given by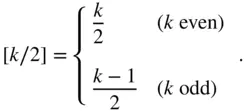

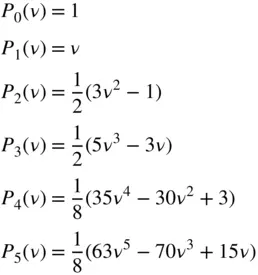
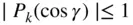(2.83)

The first few Legendre polynomials are the following:

(2.84)

Clearly the Legendre polynomials satisfy the condition , which implies that the series in Eq. (2.81)is convergent. Therefore, one can approximate the integrand of Eq. (2.78)by retaining only a finite number of terms in the series.

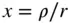By writing and 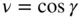, the general expression for the Legendre polynomials is given in terms of the following generating function , :

(2.85)

The generating function can be used to establish some of the basic properties of the Legendre polynomials, such as the following:

(2.86)

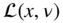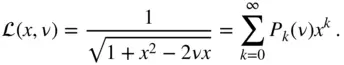
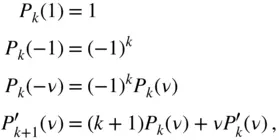
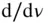where the prime stands for the derivative with respect to the argument, . The generating function, 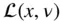, is also used to generate a Legendre polynomial from those of lower degrees with the help of recurrence formulae , such as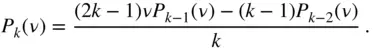

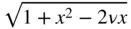(2.87)

The reciprocal of the generating function, , can be regarded as the radical portion, 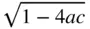, of the real root, 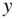, to the following quadratic equation: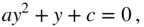

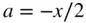(2.88)

where the positive sign is taken to correspond to the smaller of the two roots. The choice and 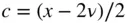yields