Robert Bartoszynski - Probability and Statistical Inference

A much more complete presentation of combinatorial methods and their applications to probability can be found in Feller (1968).

Consider two operations of some sort, which can be performed one after another. Leaving the notion of “operation” vague at the moment, we can make two assumptions:

1 The first operation can be performed in different ways.

2 For each of the ways of performing the first operation, the second operation can be performed in ways.

We have the following theorem:

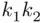Theorem 3.2.1 Under assumptions 1 and 2, a two‐step procedure consisting of a first operation followed by the second operation can be performed in distinct ways.

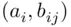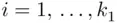Proof : Observe that each way of performing the two operations can be represented as a pair with and 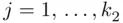, where 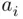is the 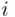th way of performing the first operation and 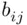is the 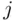th way of performing the second operation if the first operation was performed in 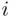th way. All such pairs can be arranged in a rectangular array with 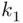rows and 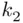columns.

We will now show some applications of Theorem 3.2.1.

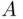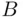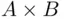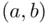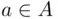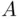One of the most common operations on sets is the Cartesian product. If and are two sets, their Cartesian product is defined as the set of all ordered pairs , where and . For instance, if consists of elements 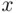and 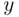, while 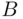consists of the digits 1, 2, and 3, then the Cartesian product 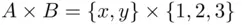contains the six pairs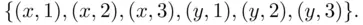

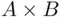(3.1)

Observe that the Cartesian product is an operation quite distinct from the set‐theoretical product . For instance, in the above case, 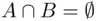, since 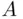and 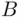have no elements in common. Also, while 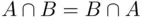, for Cartesian products in general. In cases when there is no danger of confusion, we will use the term product for Cartesian product .

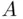Identifying now the first and second operation with “choice of an element from set ” and “choice of an element from set 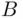,” we obtain the following consequence of Theorem 3.2.1:

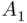Theorem 3.2.2 (Multiplication Rule) If and 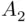are finite sets consisting, respectively, of 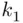and 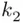elements, then the Cartesian product consists of 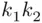elements.