An approximation to 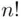 is given by the so‐called Stirling's formula.
is given by the so‐called Stirling's formula.
Theorem 3.4.3 (Stirling's Formula) We have
(3.29) 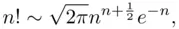
where the sign 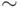 means that the ratio of the two sides tends to 1 as
means that the ratio of the two sides tends to 1 as 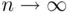 .
.
We shall not give the proof here, but interested readers can find it in more advanced texts, for example, in Chow and Teicher (1997).
A group of 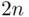 boys and
boys and 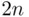 girls is divided at random into two equal parts. What is the probability
girls is divided at random into two equal parts. What is the probability 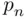 and its approximation for large
and its approximation for large 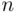 , that boys and girls are divided evenly between the two groups?
, that boys and girls are divided evenly between the two groups?
Clearly, the number of ways a group can be divided into two equal parts is 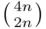 . The number of ways
. The number of ways 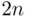 boys can be divided evenly is
boys can be divided evenly is 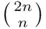 and the same holds for girls. Thus,
and the same holds for girls. Thus,
(3.30) 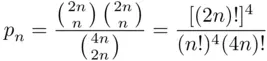
which, based on ( 3.29), can be approximated by
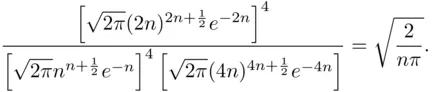
For example, in the case of 16 boys and 16 girls 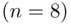 , the approximate chances of dividing both sexes evenly are about
, the approximate chances of dividing both sexes evenly are about 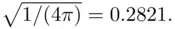 The exact value is 0.2756.
The exact value is 0.2756.
1 3.4.1 Show that if then(i) Use the definition of binomial coefficients as ratios of the factorials. (ii) Use directly the interpretation of the binomial coefficients as the number of subsets of a given size. (iii) How many ways can one choose an ‐element subset from a ‐element subset from a ‐element subset from a ‐element subset from a element set? (where ).
2 3.4.2 Find the coefficient of the term in the expansion of .
3 3.4.3 Use the argument analogous to that in Theorem 3.3.2to show that if , and , then
4 3.4.4 Use Stirling's formula to approximate the number of ways: (i) A set of size can be partitioned into two equal parts. (ii) A set of size can be partitioned into three equal parts.
5 3.4.5 Approximate the probability that every state will be represented in the committee in Problem 3.3.1(i).
1 1The integer part of , [], is the largest integer not exceeding ( etc.).
2 2This property, called exchangeability of events, will be discussed in more detail in Section 4.6.
3 3The discarded cards are not mixed with the deck. Assume that the player receives the replacement of the discarded cards from the unused remainder of the deck.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

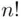 is given by the so‐called Stirling's formula.
is given by the so‐called Stirling's formula.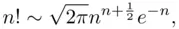
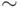 means that the ratio of the two sides tends to 1 as
means that the ratio of the two sides tends to 1 as 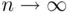 .
. boys and
boys and 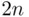 girls is divided at random into two equal parts. What is the probability
girls is divided at random into two equal parts. What is the probability 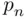 and its approximation for large
and its approximation for large 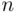 , that boys and girls are divided evenly between the two groups?
, that boys and girls are divided evenly between the two groups?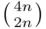 . The number of ways
. The number of ways 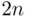 boys can be divided evenly is
boys can be divided evenly is 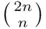 and the same holds for girls. Thus,
and the same holds for girls. Thus,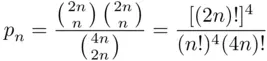
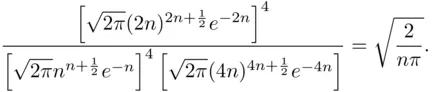
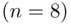 , the approximate chances of dividing both sexes evenly are about
, the approximate chances of dividing both sexes evenly are about 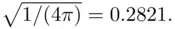 The exact value is 0.2756.
The exact value is 0.2756.










