Robert Bartoszynski - Probability and Statistical Inference

Figure 3.2Process of counting votes.

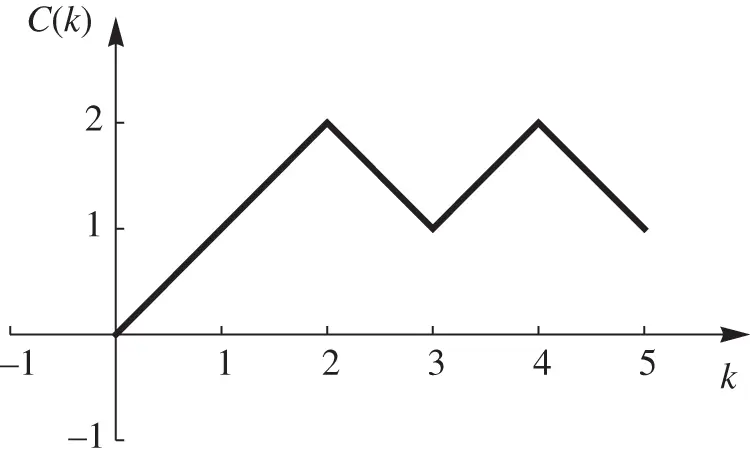
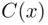In Figure 3.2, we have the beginning of counting, when the first five votes inspected are AABAB. The problem can now be formulated as finding the probability that the counting function lies above the 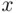‐axis for all 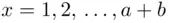. Observe that the first vote counted must be for A (as in Figure 3.2); this occurs with probability .

Figure 3.3Reflection principle.

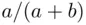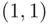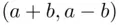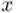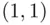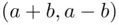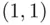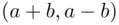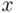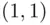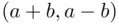The remaining votes will give a polygonal line leading from to , and we must find the number of such lines that will never touch or cross the ‐axis. The number of such lines is equal to the total number of lines from to minus the number of lines from to which touch or cross the ‐axis. The total number of lines leading from to is 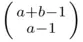, since each such line has steps “up” and steps “down,” which can be ordered in any manner. 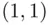Thus, it remains to count the number of lines from to 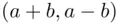that touch or cross the 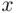‐axis. Let 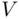be the set of all such lines. 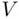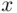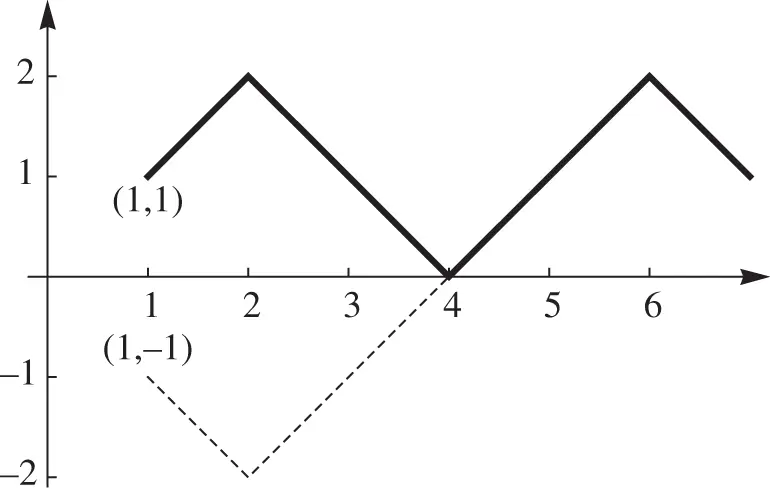Each line in must touch the ‐axis for the first time at some point, say 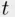(see Figure 3.3). If we reflect the part of this line that lies to the left of 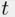with respect to 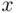‐axis, we obtain a line leading from 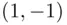to 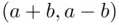. Moreover, different lines in 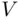will correspond to different lines leading from to 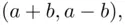and each line in the latter set will be obtained from some line in 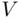. This means that the set 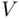has the same number of lines as the set of lines leading from 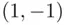to 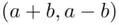. But the latter set contains 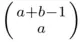lines, since each such line must have 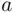steps “up” and steps “down.” Consequently, the required probability equals