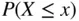1 COVER
2 TITLE PAGE
3 COPYRIGHT
4 DEDICATION
5 PREFACE
6 ACKNOWLEDGMENTS
7 ABOUT THE COMPANION WEBSITE
8 INTRODUCTION I.1 Walking the Web I.2 Benford's Law I.3 Searching the Genome I.4 Big Data I.5 From Application to Theory
9 1 FIRST PRINCIPLES 1.1 RANDOM EXPERIMENT, SAMPLE SPACE, EVENT 1.2 WHAT IS A PROBABILITY? 1.3 PROBABILITY FUNCTION 1.4 PROPERTIES OF PROBABILITIES 1.5 EQUALLY LIKELY OUTCOMES 1.6 COUNTING I 1.7 COUNTING II 1.8 PROBLEM-SOLVING STRATEGIES: COMPLEMENTS AND INCLUSION–EXCLUSION 1.9 A FIRST LOOK AT SIMULATION 1.10 SUMMARY EXERCISES
10 2 CONDITIONAL PROBABILITY AND INDEPENDENCE 2.1 CONDITIONAL PROBABILITY 2.2 NEW INFORMATION CHANGES THE SAMPLE SPACE 2.3 FINDING P(A AND B) 2.4 CONDITIONING AND THE LAW OF TOTAL PROBABILITY 2.5 BAYES FORMULA AND INVERTING A CONDITIONAL PROBABILITY 2.6 INDEPENDENCE AND DEPENDENCE 2.7 PRODUCT SPACES 2.8 SUMMARY EXERCISES
11 3 INTRODUCTION TO DISCRETE RANDOM VARIABLES 3.1 RANDOM VARIABLES 3.2 INDEPENDENT RANDOM VARIABLES 3.3 BERNOULLI SEQUENCES 3.4 BINOMIAL DISTRIBUTION 3.5 POISSON DISTRIBUTION 3.6 SUMMARY EXERCISES
12 4 EXPECTATION AND MORE WITH DISCRETE RANDOM VARIABLES 4.1 EXPECTATION 4.2 FUNCTIONS OF RANDOM VARIABLES 4.3 JOINT DISTRIBUTIONS 4.4 INDEPENDENT RANDOM VARIABLES 4.5 LINEARITY OF EXPECTATION 4.6 VARIANCE AND STANDARD DEVIATION 4.7 COVARIANCE AND CORRELATION 4.8 CONDITIONAL DISTRIBUTION 4.9 PROPERTIES OF COVARIANCE AND CORRELATION 4.10 EXPECTATION OF A FUNCTION OF A RANDOM VARIABLE 4.11 SUMMARY EXERCISES
13 5 MORE DISCRETE DISTRIBUTIONS AND THEIR RELATIONSHIPS 5.1 GEOMETRIC DISTRIBUTION 5.2 MOMENT-GENERATING FUNCTIONS 5.3 NEGATIVE BINOMIAL—UP FROM THE GEOMETRIC 5.4 HYPERGEOMETRIC—SAMPLING WITHOUT REPLACEMENT 5.5 FROM BINOMIAL TO MULTINOMIAL 5.6 BENFORD'S LAW 5.7 SUMMARY EXERCISES
14 6 CONTINUOUS PROBABILITY 6.1 PROBABILITY DENSITY FUNCTION 6.2 CUMULATIVE DISTRIBUTION FUNCTION 6.3 EXPECTATION AND VARIANCE 6.4 UNIFORM DISTRIBUTION 6.5 EXPONENTIAL DISTRIBUTION 6.6 JOINT DISTRIBUTIONS 6.7 INDEPENDENCE 6.8 COVARIANCE, CORRELATION 6.9 SUMMARY EXERCISES
15 7 CONTINUOUS DISTRIBUTIONS 7.1 NORMAL DISTRIBUTION 7.2 GAMMA DISTRIBUTION 7.3 POISSON PROCESS 7.4 BETA DISTRIBUTION 7.5 PARETO DISTRIBUTION 7.6 SUMMARY EXERCISES
16 8 DENSITIES OF FUNCTIONS OF RANDOM VARIABLES 8.1 DENSITIES VIA CDFS 8.2 MAXIMUMS, MINIMUMS, AND ORDER STATISTICS 8.3 CONVOLUTION 8.4 GEOMETRIC PROBABILITY 8.5 TRANSFORMATIONS OF TWO RANDOM VARIABLES 8.6 SUMMARY EXERCISES
17 9 CONDITIONAL DISTRIBUTION, EXPECTATION, AND VARIANCE INTRODUCTION 9.1 CONDITIONAL DISTRIBUTIONS 9.2 DISCRETE AND CONTINUOUS: MIXING IT UP 9.3 CONDITIONAL EXPECTATION 9.4 COMPUTING PROBABILITIES BY CONDITIONING 9.5 CONDITIONAL VARIANCE 9.6 BIVARIATE NORMAL DISTRIBUTION 9.7 SUMMARY EXERCISES
18 10 LIMITS 10.1 WEAK LAW OF LARGE NUMBERS 10.2 STRONG LAW OF LARGE NUMBERS 10.3 METHOD OF MOMENTS 10.4 MONTE CARLO INTEGRATION 10.5 CENTRAL LIMIT THEOREM 10.6 A PROOF OF THE CENTRAL LIMIT THEOREM 10.7 SUMMARY EXERCISES
19 11 BEYOND RANDOM WALKS AND MARKOV CHAINS 11.1 RANDOM WALKS ON GRAPHS 11.2 RANDOM WALKS ON WEIGHTED GRAPHS AND MARKOV CHAINS 11.3 FROM MARKOV CHAIN TO MARKOV CHAIN MONTE CARLO 11.4 SUMMARY EXERCISES
20 APPENDIX A: PROBABILITY DISTRIBUTIONS IN R
21 APPENDIX B: SUMMARY OF PROBABILITY DISTRIBUTIONS
22 APPENDIX C: MATHEMATICAL REMINDERS
23 APPENDIX D: WORKING WITH JOINT DISTRIBUTIONS
24 SOLUTIONS TO EXERCISESSOLUTIONS FOR CHAPTER 1 SOLUTIONS FOR CHAPTER 2 SOLUTIONS FOR CHAPTER 3 SOLUTIONS FOR CHAPTER 4 SOLUTIONS FOR CHAPTER 5 SOLUTIONS FOR CHAPTER 6 SOLUTIONS FOR CHAPTER 7 SOLUTIONS FOR CHAPTER 8 SOLUTIONS FOR CHAPTER 9 SOLUTIONS FOR CHAPTER 10 SOLUTIONS FOR CHAPTER 11
25 REFERENCES
26 INDEX
27 END USER LICENSE AGREEMENT
1 Chapter 1 TABLE 1.1. Probability model for majors. TABLE 1.2. Events and sets. TABLE 1.3. Correspondence between subsets and binary lists. TABLE 1.4. Common values of binomial coefficients. TABLE 1.5. Voting outcomes for the ballot problem.
2 Chapter 2 TABLE 2.1. Birthday probabilities.TABLE 2.2. Hypothetical 10,000 table.TABLE 2.3. Hypothetical 1000 table for color blindness.TABLE 2.4. Distribution of blood type in the United States.
3 Chapter 3TABLE 3.1. Probability distribution for the sum of two dice.TABLE 3.2. Distribution of number of children in US households.TABLE 3.3. Nucleotide frequencies in human DNA.TABLE 3.4. Deaths by horse kicks in the Prussian cavalry.TABLE 3.5. Bomb hits over London during World War II.TABLE 3.6. No-hitter baseball games
4 Chapter 4TABLE 4.1. Discrete probability distributions.TABLE 4.2. Tile values in Scrabble.TABLE 4.3. Distribution of US households by number of TVs.TABLE 4.4. Fixed points of permutations for 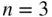 .TABLE 4.5. Household size by vehicles available.
.TABLE 4.5. Household size by vehicles available.
5 Chapter 5TABLE 5.1. Lengths of 112 World Series, 1903–2019.TABLE 5.2. Distribution of colors in a bag of candies.TABLE 5.3. Genotype frequencies for a sample of 60 fruit flies.TABLE 5.4. Benford's law.
6 Chapter 7TABLE 7.1. Comparison of tail probabilities for normal and Pareto distributions...TABLE 7.2. SAT statistics for 2011 college-bound seniors
7 Chapter 10TABLE 10.1. Grade distribution for AP examsTABLE 10.2. Monte Carlo approximation of the mean of a uniform distribution. Co...
8 Chapter 11TABLE 11.1. Simple random walk for the cycle graph on nine vertices after steps...
9 Appendix ATABLE A.1. Probability distributions in R.
1 Introduction FIGURE I.1: Benford's law describes the frequencies of first digits for many...
2 Chapter 1 FIGURE 1.1: Venn diagrams. FIGURE 1.2: Venn diagram. FIGURE 1.3: Pascal's triangle. FIGURE 1.4: Illustrating the correspondence between “bad” lists that start w... FIGURE 1.5: Venn diagram.
3 Chapter 2 FIGURE 2.1: FIGURE 2.2: Tree diagram for picking two balls from a bag of two red and thr... FIGURE 2.3: Tree diagram for Example 2.7. FIGURE 2.4: Tree diagram for blackjack. FIGURE 2.5: Solving the birthday problem with a tree diagram. FIGURE 2.6: The events  partition the sample space. The circle represents e...FIGURE 2.7: Nontransitive dice.
partition the sample space. The circle represents e...FIGURE 2.7: Nontransitive dice.
4 Chapter 3FIGURE 3.1: Four examples of the binomial distribution.FIGURE 3.2: Three random graphs on 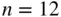 vertices generated, respectively, with FIGURE 3.3: Four Poisson distributions with varying
vertices generated, respectively, with FIGURE 3.3: Four Poisson distributions with varying 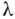 .
.
5 Chapter 4FIGURE 4.1: Four distributions with 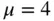 . Variances are (a) 0, (b) 2.08, (c) 4,...FIGURE 4.2: Simulation of Poisson(25) distribution. Vertical lines are drawn...FIGURE 4.3: Covariance is a measure of linear association between two random...FIGURE 4.4: Randomly colored six-by-six board. There are 19 one-by-one black...
. Variances are (a) 0, (b) 2.08, (c) 4,...FIGURE 4.2: Simulation of Poisson(25) distribution. Vertical lines are drawn...FIGURE 4.3: Covariance is a measure of linear association between two random...FIGURE 4.4: Randomly colored six-by-six board. There are 19 one-by-one black...
6 Chapter 5FIGURE 5.1: Graph of 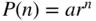 .
.
7 Chapter 6FIGURE 6.1: Density with shaded area indicating 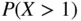 .FIGURE 6.2: Three density shapes.FIGURE 6.3: Density function and cdf.FIGURE 6.4: Cumulative distribution function
.FIGURE 6.2: Three density shapes.FIGURE 6.3: Density function and cdf.FIGURE 6.4: Cumulative distribution function 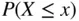
Читать дальше

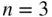 .TABLE 4.5. Household size by vehicles available.
.TABLE 4.5. Household size by vehicles available. partition the sample space. The circle represents e...FIGURE 2.7: Nontransitive dice.
partition the sample space. The circle represents e...FIGURE 2.7: Nontransitive dice.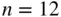 vertices generated, respectively, with FIGURE 3.3: Four Poisson distributions with varying
vertices generated, respectively, with FIGURE 3.3: Four Poisson distributions with varying 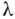 .
.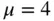 . Variances are (a) 0, (b) 2.08, (c) 4,...FIGURE 4.2: Simulation of Poisson(25) distribution. Vertical lines are drawn...FIGURE 4.3: Covariance is a measure of linear association between two random...FIGURE 4.4: Randomly colored six-by-six board. There are 19 one-by-one black...
. Variances are (a) 0, (b) 2.08, (c) 4,...FIGURE 4.2: Simulation of Poisson(25) distribution. Vertical lines are drawn...FIGURE 4.3: Covariance is a measure of linear association between two random...FIGURE 4.4: Randomly colored six-by-six board. There are 19 one-by-one black...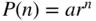 .
.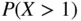 .FIGURE 6.2: Three density shapes.FIGURE 6.3: Density function and cdf.FIGURE 6.4: Cumulative distribution function
.FIGURE 6.2: Three density shapes.FIGURE 6.3: Density function and cdf.FIGURE 6.4: Cumulative distribution function