1 Cover
2 Preface to the Second Edition
3 Preface to the First Edition
4 Acknowledgments
5 About the Companion Website
6 Part I: The R Language 1 Basics of R 1.1 What Is R? 1.2 Installing R 1.3 R Documentation 1.4 Basics 1.5 Getting Help 1.6 Data Entry 1.7 Missing Values 1.8 Editing 1.9 Tidying Up 1.10 Saving and Retrieving 1.11 Packages 1.12 Interfaces 1.13 Project Reference 2 Summarizing Statistical Data 2.1 Measures of Central Tendency 2.2 Measures of Dispersion 2.3 Overall Summary Statistics 2.4 Programming in R 2.5 Project 3 Graphical Displays 3.1 BOXPLOTS 3.2 HISTOGRAMS 3.3 STEM AND LEAF 3.4 SCATTER PLOTS 3.5 THE LINE OF BEST FIT 3.6 MACHINE LEARNING AND THE LINE OF BEST FIT 3.7 GRAPHICAL DISPLAYS VERSUS SUMMARY STATISTICS 3.8 Projects References
7 Part II: Fundamentals of Probability 4 Probability Basics 4.1 Experiments, Sample Spaces, and Events 4.2 Classical Approach to Probability 4.3 Permutations and Combinations 4.4 The Birthday Problem 4.5 Balls and Bins 4.6 R Functions for Allocation 4.7 Allocation Overload 4.8 Relative Frequency Approach to Probability 4.9 Simulating Probabilities 4.10 Projects Recommended Reading 5 Rules of Probability 5.1 Probability and Sets 5.2 Mutually Exclusive Events 5.3 Complementary Events 5.4 Axioms of Probability 5.5 Properties of Probability Supplementary Reading 6 Conditional Probability 6.1 Multiplication Law of Probability 6.2 Independent Events 6.3 Independence of More than Two Events 6.4 The Intel FIASCO 6.5 Law of Total Probability 6.6 Trees 6.7 Project Note 7 Posterior Probability and Bayes 7.1 Bayes' Rule 7.2 Hardware Fault Diagnosis 7.3 Machine Learning and Classification 7.4 Spam Filtering 7.5 Machine Translation Reference 8 Reliability 8.1 Series Systems 8.2 Parallel Systems 8.3 Reliability of a System 8.4 Series–Parallel Systems 8.5 The Design of Systems 8.6 The General System
8 Part III: Discrete Distributions 9 Introduction to Discrete Distributions 9.1 Discrete Random Variables 9.2 Cumulative Distribution Function 9.3 Some Simple Discrete Distributions 9.4 Benford's Law 9.5 Summarizing Random Variables: Expectation 9.6 Properties of Expectations 9.7 Simulating Discrete Random Variables and Expectations 9.8 Bivariate Distributions 9.9 Marginal Distributions 9.10 Conditional Distributions 9.11 Project References 10 The Geometric Distribution 10.1 GEOMETRIC RANDOM VARIABLES 10.2 CUMULATIVE DISTRIBUTION FUNCTION 10.3 THE QUANTILE FUNCTION 10.4 GEOMETRIC EXPECTATIONS 10.5 SIMULATING GEOMETRIC PROBABILITIES AND EXPECTATIONS 10.6 AMNESIA 10.7 SIMULATING MARKOV 10.8 PROJECTS 11 The Binomial Distribution 11.1 Binomial Probabilities 11.2 Binomial Random Variables 11.3 Cumulative Distribution Function 11.4 The Quantile Function 11.5 Reliability: The General System 11.6 Machine Learning 11.7 Binomial Expectations 11.8 Simulating Binomial Probabilities and Expectations 11.9 Projects 12 The Hypergeometric Distribution 12.1 Hypergeometric Random Variables 12.2 Cumulative Distribution Function 12.3 The Lottery 12.4 Hypergeometric or Binomial? 12.5 Projects 13 The Poisson Distribution 13.1 Death by Horse Kick 13.2 Limiting Binomial Distribution 13.3 Random Events in Time and Space 13.4 Probability Density Function 13.5 Cumulative Distribution Function 13.6 The Quantile Function 13.7 Estimating Software Reliability 13.8 Modeling Defects In Integrated Circuits 13.9 Simulating Poisson Probabilities 13.10 Projects References 14 Sampling Inspection Schemes14.1 Introduction 14.2 Single Sampling Inspection Schemes 14.3 Acceptance Probabilities 14.4 Simulating Sampling Inspection Schemes 14.5 Operating Characteristic Curve 14.6 Producer's and Consumer's Risks 14.7 Design of Sampling Schemes 14.8 Rectifying Sampling Inspection Schemes 14.9 Average Outgoing Quality 14.10 Double Sampling Inspection Schemes 14.11 Average Sample Size 14.12 Single Versus Double Schemes 14.13 Projects
9 Part IV: Continuous Distributions 15 Introduction to Continuous Distributions 15.1 Introduction to Continuous Random Variables 15.2 Probability Density Function 15.3 Cumulative Distribution Function 15.4 The Uniform Distribution 15.5 Expectation of a Continuous Random Variable 15.6 Simulating Continuous Variables 16 The Exponential Distribution16.1 Modeling Waiting Times 16.2 Probability Density Function of Waiting Times 16.3 Cumulative Distribution Function 16.4 Modeling Lifetimes 16.5 Quantiles 16.6 Exponential Expectations 16.7 Simulating Exponential Probabilities and Expectations 16.8 Amnesia 16.9 Simulating Markov 16.10 Project 17 Queues 17.1 The Single Server Queue 17.2 Traffic Intensity 17.3 Queue Length 17.4 Average Response Time 17.5 Extensions of the M/M/1 Queue 17.6 Project Reference Notes 18 The Normal Distribution 18.1 The Normal Probability Density Function 18.2 The Cumulative Distribution Function 18.3 Quantiles 18.4 The Standard Normal Distribution 18.5 Achieving Normality: Limiting Distributions 18.6 Projects 19 Process Control 19.1 Control Charts 19.2 Cusum Charts 19.3 Charts for Defective Rates 19.4 Project
10 Part V: Tailing Off 20 The Inequalities of Markov and Chebyshev 20.1 Markov's Inequality 20.2 Algorithm Runtime 20.3 Chebyshev's Inequality
11 Appendix A: Data: Examination Results
12 Appendix B: The Line of Best Fit: Coefficient Derivations
13 Appendix C: Variance Derivations C.1 Variance of the Geometric Distribution (Chapter 10) C.2 Variance of the Binomial Distribution (Chapter 11) C.3 Variance of the Poisson Distribution (Chapter 13) C.4 Variance of the Uniform Distribution (Chapter 15) C.5 Variance of the Exponential Distribution (Chapter 16)
14 Appendix D: Binomial Approximation to the Hypergeometric
15 Appendix E: Normal Tables
16 Appendix F: The Inequalities of Markov and ChebyshevF.1 Markov's Inequality: A Proof Without Words F.2 Chebyshev's Inequality: Markov's in Disguise
17 Index to R Commands
18 Index
19 Postface
20 End User License Agreement
1 Chapter 3 TABLE 3.1 The Training Set TABLE 3.2 The Testing Set TABLE 3.3 The Anscombe Quartet
2 Chapter 4TABLE 4.1 ProgramsTABLE 4.2 Birthday Probabilities
3 Chapter 5TABLE 5.1 Sets and Events
4 Chapter 9TABLE 9.1 Benford's First DigitsTABLE 9.2 Joint Distribution of Errors in ProgramsTABLE 9.3 Rolling Two DiceTABLE 9.4 Joint Distribution of Hardware FailuresTABLE 9.5 Marginal Distributions of Hardware FailuresTABLE 9.6 Conditional Distributions of Hardware Failures in Lab 1 ( 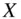 ) TABLE 9.7 Conditional Distributions of Hardware Failures in Lab 2 (
) TABLE 9.7 Conditional Distributions of Hardware Failures in Lab 2 ( 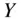 )
)
5 Chapter 10TABLE 10.1 Simulation Comparisons of the Geometric pdf
6 Chapter 11TABLE 11.1 Binomial Probabilities with 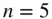 and
and 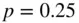
7 Chapter 12TABLE 12.1 Hypergeometric and Binomial Probabilities with 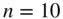 and
and 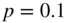
8 Chapter 13TABLE 13.1 Horse Kick Fatalities in the Prussian CavalryTABLE 13.2 Estimating Fatal Horse KicksTABLE 13.3 Binomial and Poisson Probabilities
9 Chapter 14TABLE 14.1 Producer's and Consumer's RisksTABLE 14.2 Average Outgoing QualityTABLE 14.3 Acceptance ProbabilitiesTABLE 14.4 Average Sample SizeTABLE 14.5 Average Outgoing Quality
Читать дальше

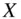 ) TABLE 9.7 Conditional Distributions of Hardware Failures in Lab 2 (
) TABLE 9.7 Conditional Distributions of Hardware Failures in Lab 2 ( 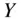 )
)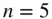 and
and 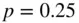
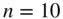 and
and