In the average hospital, many terabytes (1 terabyte = 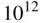 bytes) of digital magnetic resonance imaging (MRI) data are generated each year. A half-hour MRI scan might collect 100 Mb of data. These data are then compressed to a smaller image, say 5 Mb, with little loss of clarity or detail. Medical and most natural images are compressible since lots of pixels have similar values. Compression algorithms work by essentially representing the image as a sum of simple functions (such as sine waves) and then discarding those terms that have low information content. This is a fundamental idea in signal processing, and essentially what is done when you take a picture on your cell phone and then convert it to a JPEG file for sending to a friend or uploading to the web.
bytes) of digital magnetic resonance imaging (MRI) data are generated each year. A half-hour MRI scan might collect 100 Mb of data. These data are then compressed to a smaller image, say 5 Mb, with little loss of clarity or detail. Medical and most natural images are compressible since lots of pixels have similar values. Compression algorithms work by essentially representing the image as a sum of simple functions (such as sine waves) and then discarding those terms that have low information content. This is a fundamental idea in signal processing, and essentially what is done when you take a picture on your cell phone and then convert it to a JPEG file for sending to a friend or uploading to the web.
Compressed sensing asks: If the data are ultimately compressible, is it really necessary to acquire all the data in the first place? Can just the final compressed data be what is initially gathered? And the startling answer is that by randomly sampling the object of interest, the final image can be reconstructed with similar results as if the object had been fully sampled. Random sampling of MRI scans produces an image of similar quality as when the entire object is scanned. The new technique has reduced MRI scan time to one-seventh the original time, from about half an hour to less than 5 minutes, and shows enormous promise for many other applied areas. For more information on this topic, the reader is directed to Mackenzie [2009].
I.5 From Application to Theory
Having sung the praises of applications and case studies, we come back to the importance of theory.
Probability has been called the science of uncertainty. “Mathematical probability” may seem an oxymoron like jumbo shrimp or civil war. If any discipline can profess a claim of “certainty,” surely it is mathematics with its adherence to rigorous proof and timeless results.
One of the great achievements of modern mathematics was putting the study of probability on a solid scientific foundation. This was done in the 1930s, when the Russian mathematician Andrey Nikolaevich Kolmogorov built up probability theory in a rigorous way similarly to how Euclid built up geometry. Much of his work is the material of a graduate-level course, but the basic framework of axiom, definition, theory, and proof sets the framework for the modern treatment of the subject.
One of the joys of learning probability is the compelling imagery we can exploit. Geometers draw circles and squares; probabilists toss coins and roll dice. There is no perfect circle in the physical universe. And the “fair coin” is an idealized model. Yet when you take real pennies and toss them repeatedly, the results conform so beautifully to the theory.
In this book, we use the computer program R. Ris free software and an interactive computing environment available for download at http://www.r-project.org/. If you have never used Rbefore, we encourage you to work through the introductory Rsupplement to familiarize yourself with the language. As you work through the text, the associated supplements support working with the code and script files. The script files only require R. For working with the supplements, you can read the pdf versions, or if you want to run the code yourself, we recommend using RStudio to open these RMarkdown files. RStudio has a free version, and it provides a useful user interface for R. RMarkdown files allow Rcode to be interwoven with text in a reproducible fashion.
Simulation plays a significant role in this book. Simulation is the use of random numbers to generate samples from a random experiment. Today, it is a bedrock tool in the sciences and data analysis. Many problems that were for all practical purposes impossible to solve before the computer age are now easily handled with simulation.
There are many compelling reasons for including simulation in a probability course. Simulation helps build invaluable intuition for how random phenomena behave. It will also give you a flexible platform to test how changes in assumptions and parameters can affect outcomes. And the exercise of translating theoretical models into usable simulation code (easy to do in R) will make the subject more concrete and hopefully easier to understand.
And, most importantly, it is fun! Students enjoy the hands-on approach to the subject that simulation offers. It is thrilling to see some complex theoretical calculation “magically” verified by a simulation.
To succeed in this subject, read carefully, work through the examples, and do as many problems as you can. But most of all, enjoy the ride!
The results concerning fluctuations in coin tossing show that widely held beliefs …are fallacious. They are so amazing and so at variance with common intuition that even sophisticated colleagues doubted that coins actually misbehave as theory predicts. The record of a simulated experiment is therefore included….
—William Feller, An Introduction to Probability Theory and Its Applications , Vol. 1, Third Edition (1968), page xi.
The beginning is the most important part of the work.
—Plato
1 Define basic probability and set theory terms.
2 Give examples of sample spaces, events, and probability models.
3 Apply properties of probability functions.
4 Solve problems involving equally likely outcomes and using counting methods.
5 (C) Explore simulation basics in R with a focus on reproducibility.
1.1 RANDOM EXPERIMENT, SAMPLE SPACE, EVENT
Probability begins with some activity, process, or experiment whose outcome is uncertain. This can be as simple as throwing dice or as complicated as tomorrow's weather.
Given such a “random experiment,” the set of all possible outcomes is called the sample space . We will use the Greek capital letter 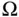 (omega) to represent the sample space.
(omega) to represent the sample space.
Perhaps the quintessential random experiment is flipping a coin. Suppose a coin is tossed three times. Let H represent heads and T represent tails. The sample space is
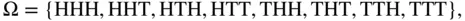
consisting of eight outcomes. The Greek lowercase omega 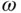 will be used to denote these outcomes, the elements of
will be used to denote these outcomes, the elements of 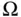 .
.
An event is a set of outcomes, and as such is a subset of the sample space 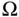 . Often, we refer to events by assigning them a capital letter near the beginning of the alphabet, such as event
. Often, we refer to events by assigning them a capital letter near the beginning of the alphabet, such as event 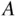 . The event of getting all heads in three coin tosses can be written as
. The event of getting all heads in three coin tosses can be written as
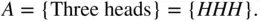
Event 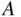 contains a single outcome, and clearly,
contains a single outcome, and clearly, 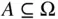 . More commonly, events include multiple outcomes. The event of getting at least two tails is
. More commonly, events include multiple outcomes. The event of getting at least two tails is
Читать дальше

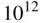 bytes) of digital magnetic resonance imaging (MRI) data are generated each year. A half-hour MRI scan might collect 100 Mb of data. These data are then compressed to a smaller image, say 5 Mb, with little loss of clarity or detail. Medical and most natural images are compressible since lots of pixels have similar values. Compression algorithms work by essentially representing the image as a sum of simple functions (such as sine waves) and then discarding those terms that have low information content. This is a fundamental idea in signal processing, and essentially what is done when you take a picture on your cell phone and then convert it to a JPEG file for sending to a friend or uploading to the web.
bytes) of digital magnetic resonance imaging (MRI) data are generated each year. A half-hour MRI scan might collect 100 Mb of data. These data are then compressed to a smaller image, say 5 Mb, with little loss of clarity or detail. Medical and most natural images are compressible since lots of pixels have similar values. Compression algorithms work by essentially representing the image as a sum of simple functions (such as sine waves) and then discarding those terms that have low information content. This is a fundamental idea in signal processing, and essentially what is done when you take a picture on your cell phone and then convert it to a JPEG file for sending to a friend or uploading to the web.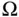 (omega) to represent the sample space.
(omega) to represent the sample space.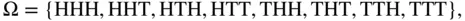
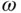 will be used to denote these outcomes, the elements of
will be used to denote these outcomes, the elements of 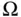 .
.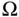 . Often, we refer to events by assigning them a capital letter near the beginning of the alphabet, such as event
. Often, we refer to events by assigning them a capital letter near the beginning of the alphabet, such as event 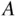 . The event of getting all heads in three coin tosses can be written as
. The event of getting all heads in three coin tosses can be written as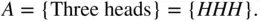
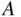 contains a single outcome, and clearly,
contains a single outcome, and clearly, 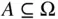 . More commonly, events include multiple outcomes. The event of getting at least two tails is
. More commonly, events include multiple outcomes. The event of getting at least two tails is










