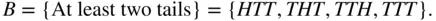
We often desire probabilities of events. But before learning how to find these probabilities, we first learn to identify the sample space and relevant event for a given problem.
Example 1.1 The weather forecast for tomorrow says rain. The number of umbrellas students bring to class can be considered an outcome of a random experiment. If at most each of students brings one umbrella, then the sample space is the set . The event that between 2 and 4 umbrellas are brought to class is
Dice are often used to illustrate probability concepts. Unless stated otherwise, in this text, rolling a die refers to rolling a fair six-sided die with the usual numeric labels of the numbers 1 through 6.
Example 1.2 Roll a pair of dice. Find the sample space and identify the event that the sum of the two dice is equal to 7.The random experiment is rolling two dice. Keeping track of the roll of each die gives the sample spaceThe event is The sample space can also be presented using an array format, where the rows denote the first roll and the columns denote the second roll. The cell entries are the sum of the row and column numbers. All 36 outcomes will be represented in the resulting cells. The event can then be identified by finding the cells that correspond to the desired criteria.
Example 1.3 Yolanda and Zach are running for president of the student association. One thousand students will be voting, and each voter will pick one of the two candidates. We will eventually ask questions like, What is the probability that Yolanda wins the election over Zach by at least 100 votes? But before actually finding this probability, first identify (i) the sample space and (ii) the event that Yolanda beats Zach by at least 100 votes.(i) The outcome of the vote can be denoted as , where is the number of votes for Yolanda, and is the number of votes for Zach. Then the sample space of all voting outcomes is(ii) Let be the event that Yolanda beats Zach by at least 100 votes. The event consists of all outcomes in which , or . That is,
Example 1.4 Diego will continue to flip a coin until heads appears. Identify the sample space and the event that it will take Diego at least three coin flips to get a head.The sample space is the set of all sequences of coin flips with one head preceded by some number of tails. That is,The desired event is . Note that in this case both the sample space and the event are infinite, meaning they contain an infinite number of outcomes.
1.2 WHAT IS A PROBABILITY?
What does it mean to say that the probability that 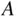 occurs or the probability of
occurs or the probability of 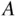 is equal to
is equal to 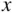 ?
?
From a formal, purely mathematical point of view, a probability is a number between 0 and 1 that satisfies certain properties, which we will describe later. From a practical, empirical point of view, a probability matches up with our intuition of the likelihood or “chance” that an event occurs. An event that has probability 0 “never” happens. An event that has probability 1 is “certain” to happen. In repeated coin flips, a fair coin comes up heads about half the time, and the probability of heads is equal to one-half.
Let 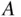 be an event associated with some random experiment. One way to understand the probability of
be an event associated with some random experiment. One way to understand the probability of 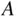 is to perform the following thought exercise: imagine conducting the experiment over and over, infinitely often, keeping track of how often
is to perform the following thought exercise: imagine conducting the experiment over and over, infinitely often, keeping track of how often 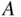 occurs. Each experiment is called a trial . If the event
occurs. Each experiment is called a trial . If the event 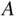 occurs when the experiment is performed, that is a success . The proportion of successes is the probability of
occurs when the experiment is performed, that is a success . The proportion of successes is the probability of 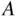 , written
, written 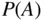 .
.
This is the relative frequency interpretation of probability, which says that the probability of an event is equal to its relative frequency in a large number of trials.
When the weather forecaster tells us that tomorrow there is a 20% chance of rain, we understand that to mean that if we could repeat today's conditions—the air pressure, temperature, wind speed, etc.—over and over again, then 20% of the resulting “tomorrows” will result in rain. Closer to what weather forecasters actually do in coming up with that 20% number, together with using satellite and radar information along with sophisticated computational models, is to go back in the historical record and find other days that match up closely with today's conditions and see what proportion of those days resulted in rain on the following day.
There are definite limitations to constructing a rigorous mathematical theory out of this intuitive and empirical view of probability. One cannot actually repeat an experiment infinitely many times. To define probability carefully, we need to take a formal, axiomatic, mathematical approach. Nevertheless, the relative frequency viewpoint will still be useful in order to gain intuitive understanding. And by the end of the book, we will actually derive the relative frequency viewpoint as a consequence of the mathematical theory.
We assume for the next several chapters that the sample space is discrete . This means that the sample space is either finite or countably infinite.
A set is countably infinite if the elements of the set can be arranged as a sequence. The natural numbers 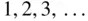 is the classic example of a countably infinite set. And all countably infinite sets can be put in one-to-one correspondence with the natural numbers.
is the classic example of a countably infinite set. And all countably infinite sets can be put in one-to-one correspondence with the natural numbers.
If the sample space is finite, it can be written as 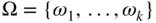 . If the sample space is countably infinite, it can be written as
. If the sample space is countably infinite, it can be written as 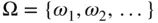 .
.
The set of all real numbers is an infinite set that is not countably infinite. It is called uncountable . An interval of real numbers, such as (0,1), the numbers between 0 and 1, is also uncountable. Probability on uncountable spaces will require differential and integral calculus and will be discussed in the second half of this book.
A probability function assigns numbers between 0 and 1 to events according to three defining properties.
Читать дальше

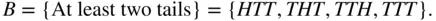
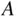 occurs or the probability of
occurs or the probability of 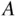 is equal to
is equal to 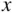 ?
?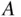 be an event associated with some random experiment. One way to understand the probability of
be an event associated with some random experiment. One way to understand the probability of 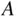 is to perform the following thought exercise: imagine conducting the experiment over and over, infinitely often, keeping track of how often
is to perform the following thought exercise: imagine conducting the experiment over and over, infinitely often, keeping track of how often 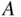 occurs. Each experiment is called a trial . If the event
occurs. Each experiment is called a trial . If the event 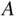 occurs when the experiment is performed, that is a success . The proportion of successes is the probability of
occurs when the experiment is performed, that is a success . The proportion of successes is the probability of 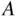 , written
, written 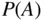 .
.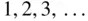 is the classic example of a countably infinite set. And all countably infinite sets can be put in one-to-one correspondence with the natural numbers.
is the classic example of a countably infinite set. And all countably infinite sets can be put in one-to-one correspondence with the natural numbers.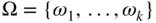 . If the sample space is countably infinite, it can be written as
. If the sample space is countably infinite, it can be written as 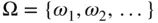 .
.










