The following theorem is an immediate consequence of Theorem 3.3.3applied to 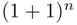 and
and 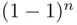 , respectively.
, respectively.
Theorem 3.3.4 The binomial coefficients satisfy the identities
(3.17) 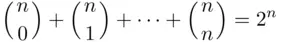
and
(3.18) 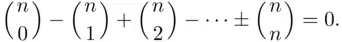
We also have the following theorem:
Theorem 3.3.5 For every 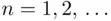 and every
and every 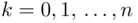
(3.19) 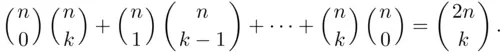
Proof : Consider the product 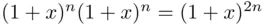 . Expanding the right‐hand side, we obtain
. Expanding the right‐hand side, we obtain
(3.20) 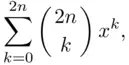
while the left‐hand side equals
(3.21) 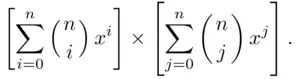
For 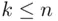 , comparison of the coefficients of
, comparison of the coefficients of 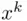 in ( 3.20) and ( 3.21) gives ( 3.19).
in ( 3.20) and ( 3.21) gives ( 3.19).
As a consequence of ( 3.19), we obtain a corollary:
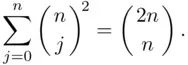
Proof : Take 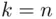 in ( 3.19) and use the fact that
in ( 3.19) and use the fact that
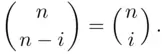
Below we present some examples of the use of binomial coefficient in solving various probability problems, some with a long history.
Let us consider a selection without replacement from a finite set containing two categories of objects. If  balls are to be selected from an urn containing
balls are to be selected from an urn containing 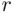 red and
red and 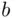 blue balls, one might want to know the probability that there will be exactly
blue balls, one might want to know the probability that there will be exactly 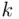 red balls chosen.
red balls chosen.
We apply here the “classical” definition of probability. The choice of 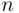 objects without replacement is the same as choosing a subset of
objects without replacement is the same as choosing a subset of 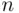 objects from the set of total of
objects from the set of total of 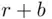 objects. This can be done in
objects. This can be done in 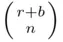 different ways. Since we must have
different ways. Since we must have 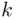 red balls, this choice can be made in
red balls, this choice can be made in 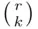 ways. Similarly,
ways. Similarly,  blue balls can be selected in
blue balls can be selected in 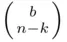 ways. As each choice of
ways. As each choice of 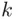 red balls can be combined with each of the
red balls can be combined with each of the 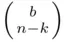 choices of blue balls then, by Theorem 3.2.2, the total number of choices is the product
choices of blue balls then, by Theorem 3.2.2, the total number of choices is the product 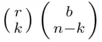 and
and
(3.22) 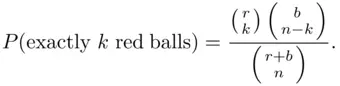
The next example shows an interesting application of formula ( 3.22).
Consider the problem of estimating the number of fish in a lake (the method described below is also used to estimate the sizes of bird or wildlife populations). The lake contains an unknown number 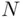 of fish. To estimate
of fish. To estimate 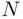 , we first catch
, we first catch 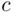 fish, label them, and release them back into the lake. We assume here that labeling does not harm fish in any way, that the labeled fish mix with unlabeled ones in a random manner, and that
fish, label them, and release them back into the lake. We assume here that labeling does not harm fish in any way, that the labeled fish mix with unlabeled ones in a random manner, and that 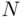 remains constant (in practice, these assumptions may be debatable). We now catch
remains constant (in practice, these assumptions may be debatable). We now catch 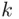 fish, and observe the number, say
fish, and observe the number, say 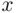 , of labeled ones among them. The values
, of labeled ones among them. The values 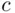 and
and  are, at least partially, under the control of the experimenter. The unknown parameter is
are, at least partially, under the control of the experimenter. The unknown parameter is 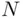 , while
, while 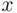 is the value occurring at random, and providing the key to estimating
is the value occurring at random, and providing the key to estimating 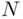 . Let us compute the probability
. Let us compute the probability 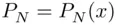 of observing
of observing 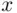 labeled fish in the second catch if there are
labeled fish in the second catch if there are 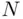 fish in the lake. We may interpret fish as balls in an urn, with labeled and unlabeled fish taking on the roles of red and blue balls. Formula ( 3.22) gives
fish in the lake. We may interpret fish as balls in an urn, with labeled and unlabeled fish taking on the roles of red and blue balls. Formula ( 3.22) gives
Читать дальше

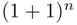 and
and 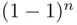 , respectively.
, respectively.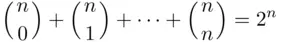
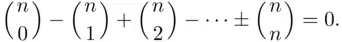
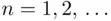 and every
and every 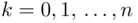
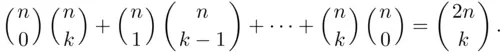
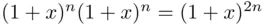 . Expanding the right‐hand side, we obtain
. Expanding the right‐hand side, we obtain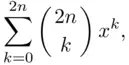
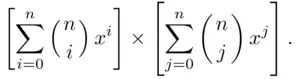
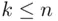 , comparison of the coefficients of
, comparison of the coefficients of 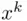 in ( 3.20) and ( 3.21) gives ( 3.19).
in ( 3.20) and ( 3.21) gives ( 3.19).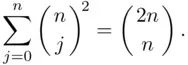
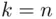 in ( 3.19) and use the fact that
in ( 3.19) and use the fact that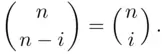
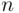 balls are to be selected from an urn containing
balls are to be selected from an urn containing 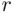 red and
red and 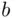 blue balls, one might want to know the probability that there will be exactly
blue balls, one might want to know the probability that there will be exactly 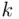 red balls chosen.
red balls chosen.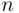 objects without replacement is the same as choosing a subset of
objects without replacement is the same as choosing a subset of 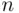 objects from the set of total of
objects from the set of total of 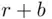 objects. This can be done in
objects. This can be done in 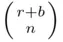 different ways. Since we must have
different ways. Since we must have 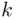 red balls, this choice can be made in
red balls, this choice can be made in 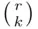 ways. Similarly,
ways. Similarly,  blue balls can be selected in
blue balls can be selected in 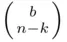 ways. As each choice of
ways. As each choice of 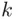 red balls can be combined with each of the
red balls can be combined with each of the 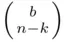 choices of blue balls then, by Theorem 3.2.2, the total number of choices is the product
choices of blue balls then, by Theorem 3.2.2, the total number of choices is the product 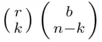 and
and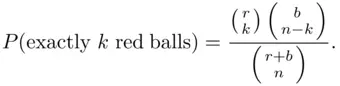
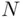 of fish. To estimate
of fish. To estimate 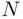 , we first catch
, we first catch 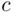 fish, label them, and release them back into the lake. We assume here that labeling does not harm fish in any way, that the labeled fish mix with unlabeled ones in a random manner, and that
fish, label them, and release them back into the lake. We assume here that labeling does not harm fish in any way, that the labeled fish mix with unlabeled ones in a random manner, and that 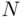 remains constant (in practice, these assumptions may be debatable). We now catch
remains constant (in practice, these assumptions may be debatable). We now catch 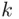 fish, and observe the number, say
fish, and observe the number, say 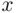 , of labeled ones among them. The values
, of labeled ones among them. The values 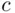 and
and  are, at least partially, under the control of the experimenter. The unknown parameter is
are, at least partially, under the control of the experimenter. The unknown parameter is 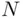 , while
, while 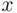 is the value occurring at random, and providing the key to estimating
is the value occurring at random, and providing the key to estimating 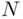 . Let us compute the probability
. Let us compute the probability 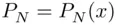 of observing
of observing 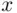 labeled fish in the second catch if there are
labeled fish in the second catch if there are 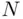 fish in the lake. We may interpret fish as balls in an urn, with labeled and unlabeled fish taking on the roles of red and blue balls. Formula ( 3.22) gives
fish in the lake. We may interpret fish as balls in an urn, with labeled and unlabeled fish taking on the roles of red and blue balls. Formula ( 3.22) gives










