Example 3.11 Matching Problem
A secretary typed 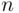 letters and addressed
letters and addressed 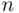 envelopes. For some reason, the letters were put into envelopes at random. What is the probability of at least one match, that is, of at least one letter being put into the correct envelope?
envelopes. For some reason, the letters were put into envelopes at random. What is the probability of at least one match, that is, of at least one letter being put into the correct envelope?
This problem appears in many textbooks under various formulations (e.g., of guests receiving their hats at random). One could expect the probability of at least one match to vary greatly with 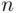 . However, the contrary is true: this probability is almost independent of
. However, the contrary is true: this probability is almost independent of  . Let
. Let 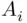 be the event that
be the event that 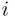 th letter is placed in the correct envelope. Using formula ( 2.6), we have
th letter is placed in the correct envelope. Using formula ( 2.6), we have
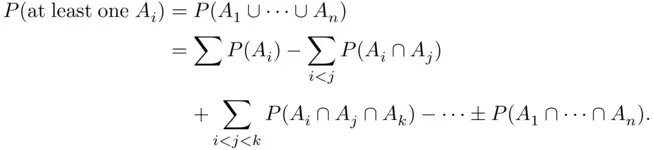
By symmetry, the probability of each intersection depends only on the number of events in the intersection, 2, so we let 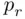 denote the probability of the intersection of
denote the probability of the intersection of 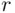 events,
events, 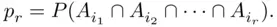 Clearly, the numbers of terms in the consecutive sums are
Clearly, the numbers of terms in the consecutive sums are
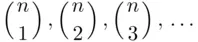
and
(3.25) 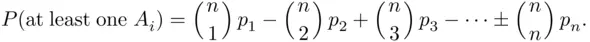
To evaluate 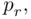 we can argue as follows: Assume that the envelopes are ordered in some way. The total number of ways one can order
we can argue as follows: Assume that the envelopes are ordered in some way. The total number of ways one can order 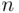 letters is
letters is 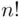 . If specific
. If specific 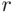 events, say
events, say  are to occur (perhaps in conjunction with other events), then the letters number
are to occur (perhaps in conjunction with other events), then the letters number  must be at their appropriate places in the ordering (to match their envelopes). The remaining
must be at their appropriate places in the ordering (to match their envelopes). The remaining  letters can appear in any of the
letters can appear in any of the 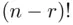 orders. Thus,
orders. Thus,
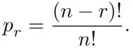
Consequently, the 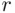 th term in the sum ( 3.25) equals (up to the sign)
th term in the sum ( 3.25) equals (up to the sign)
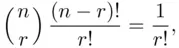
and we obtain
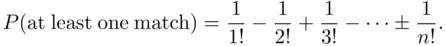
Since
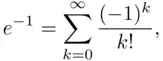
we have
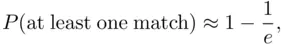
with the accuracy increasing as 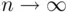 . The approximation is actually quite good for small
. The approximation is actually quite good for small 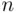 . The limiting value is 0.63212056, while the exact values of the probability
. The limiting value is 0.63212056, while the exact values of the probability 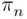 of at least one match for selected values of
of at least one match for selected values of 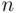 are
are

Example 3.12 Ballot Problem
Suppose that in an election, candidate A receives 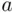 votes, while candidate B receives
votes, while candidate B receives 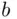 votes, where
votes, where 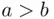 . Assuming that votes are counted in random order, what is the probability that during the whole process of counting A will be ahead of B?
. Assuming that votes are counted in random order, what is the probability that during the whole process of counting A will be ahead of B?
Note that other votes, if any, do not matter, and we may assume that 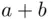 is the total number of votes. The process of counting votes is determined by the arrangement of the votes, that is, the arrangement of
is the total number of votes. The process of counting votes is determined by the arrangement of the votes, that is, the arrangement of 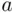 symbols A, and
symbols A, and 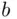 symbols B. Clearly, such an arrangement is uniquely determined by specifying the locations of the As (or, equivalently, Bs). It might be helpful to use a graphical representation: define the function
symbols B. Clearly, such an arrangement is uniquely determined by specifying the locations of the As (or, equivalently, Bs). It might be helpful to use a graphical representation: define the function 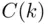 as the net count for candidate A after inspection of
as the net count for candidate A after inspection of 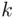 votes. Thus, if in the first
votes. Thus, if in the first 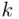 votes, we had
votes, we had 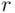 votes for A and
votes for A and  votes for B, then
votes for B, then 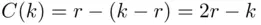 . We can then represent the process of counting as a polygonal line that starts at the origin and has vertices
. We can then represent the process of counting as a polygonal line that starts at the origin and has vertices 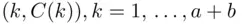 (see Figure 3.2).
(see Figure 3.2).
Читать дальше

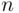 letters and addressed
letters and addressed 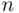 envelopes. For some reason, the letters were put into envelopes at random. What is the probability of at least one match, that is, of at least one letter being put into the correct envelope?
envelopes. For some reason, the letters were put into envelopes at random. What is the probability of at least one match, that is, of at least one letter being put into the correct envelope?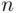 . However, the contrary is true: this probability is almost independent of
. However, the contrary is true: this probability is almost independent of  . Let
. Let 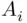 be the event that
be the event that 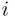 th letter is placed in the correct envelope. Using formula ( 2.6), we have
th letter is placed in the correct envelope. Using formula ( 2.6), we have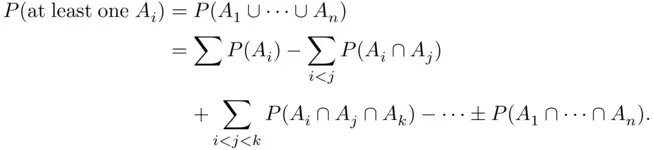
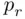 denote the probability of the intersection of
denote the probability of the intersection of 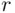 events,
events, 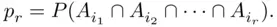 Clearly, the numbers of terms in the consecutive sums are
Clearly, the numbers of terms in the consecutive sums are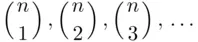
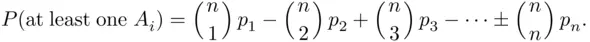
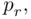 we can argue as follows: Assume that the envelopes are ordered in some way. The total number of ways one can order
we can argue as follows: Assume that the envelopes are ordered in some way. The total number of ways one can order 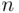 letters is
letters is 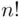 . If specific
. If specific 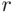 events, say
events, say  are to occur (perhaps in conjunction with other events), then the letters number
are to occur (perhaps in conjunction with other events), then the letters number  must be at their appropriate places in the ordering (to match their envelopes). The remaining
must be at their appropriate places in the ordering (to match their envelopes). The remaining  letters can appear in any of the
letters can appear in any of the 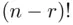 orders. Thus,
orders. Thus,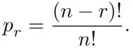
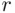 th term in the sum ( 3.25) equals (up to the sign)
th term in the sum ( 3.25) equals (up to the sign)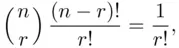
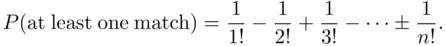
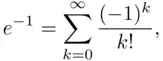
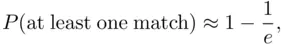
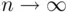 . The approximation is actually quite good for small
. The approximation is actually quite good for small 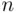 . The limiting value is 0.63212056, while the exact values of the probability
. The limiting value is 0.63212056, while the exact values of the probability 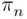 of at least one match for selected values of
of at least one match for selected values of 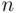 are
are
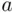 votes, while candidate B receives
votes, while candidate B receives 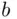 votes, where
votes, where 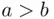 . Assuming that votes are counted in random order, what is the probability that during the whole process of counting A will be ahead of B?
. Assuming that votes are counted in random order, what is the probability that during the whole process of counting A will be ahead of B?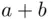 is the total number of votes. The process of counting votes is determined by the arrangement of the votes, that is, the arrangement of
is the total number of votes. The process of counting votes is determined by the arrangement of the votes, that is, the arrangement of 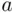 symbols A, and
symbols A, and 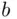 symbols B. Clearly, such an arrangement is uniquely determined by specifying the locations of the As (or, equivalently, Bs). It might be helpful to use a graphical representation: define the function
symbols B. Clearly, such an arrangement is uniquely determined by specifying the locations of the As (or, equivalently, Bs). It might be helpful to use a graphical representation: define the function 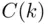 as the net count for candidate A after inspection of
as the net count for candidate A after inspection of 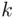 votes. Thus, if in the first
votes. Thus, if in the first 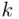 votes, we had
votes, we had 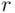 votes for A and
votes for A and  votes for B, then
votes for B, then 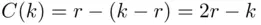 . We can then represent the process of counting as a polygonal line that starts at the origin and has vertices
. We can then represent the process of counting as a polygonal line that starts at the origin and has vertices 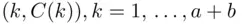 (see Figure 3.2).
(see Figure 3.2).










