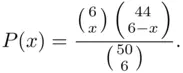
For 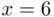 , we have
, we have
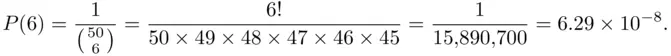
Similarly 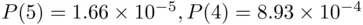 and
and 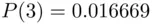 .
.
Thus, the chances of winning a share in the Big Prize are about 1 in 16 million. It would therefore appear that there should be, on average, one big winner in every 16 million tickets sold. The weekly numbers of tickets sold are well known, and it turns out that the weekly numbers of winners (of the Big Prize) vary much more than one would expect. For example, in weeks where the number of tickets sold is about 16 million, one could expect no winner, one winner, or two winners; three winners is unlikely. In reality, it is not at all uncommon to have five or more winning tickets in a week with 16 million tickets sold. These observations made some people suspicious about the honesty of the process of drawing the numbers, to the extent that there have been attempts to bring suit against the lottery (e.g., accusing the organizers of biasing the lottery balls with certain numbers so as to decrease their chance of being selected, thus favoring some other numbers).
Actually, the big variability of weekly numbers of winners is to be expected if one realizes that these numbers depend on two chance processes: the choice of winning numbers from the urn (which may be, and probably is, quite fair) and the choice of numbers by the players. This choice is definitely not uniform. It favors certain combinations, which seem more “random” to the naive persons than other choices. For instance, the combination 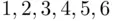 appears less likely than (say)
appears less likely than (say) 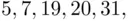 and 45. As a consequence some combinations are selected more often by the players than others. Each combination has the same chance of being the winning one, but some may have higher numbers of winners associated with them. This point can be illustrated by the following analogy: Imagine that each week a first name (Mary, Susan, George, etc.) is chosen at random from the set of all names used, and all persons in the state with the selected name share the prize. The chances of being chosen are the same for John as for Sebastian, as they depend on the process of sampling names of winners. But if the name Sebastian is chosen, each Sebastian will share the prize with many fewer other winners than if the name John were selected. Here the numbers of winners to share the prize depend on another process, namely that of parents selecting names for their children.
and 45. As a consequence some combinations are selected more often by the players than others. Each combination has the same chance of being the winning one, but some may have higher numbers of winners associated with them. This point can be illustrated by the following analogy: Imagine that each week a first name (Mary, Susan, George, etc.) is chosen at random from the set of all names used, and all persons in the state with the selected name share the prize. The chances of being chosen are the same for John as for Sebastian, as they depend on the process of sampling names of winners. But if the name Sebastian is chosen, each Sebastian will share the prize with many fewer other winners than if the name John were selected. Here the numbers of winners to share the prize depend on another process, namely that of parents selecting names for their children.
We have 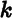 urns, labeled
urns, labeled  , and
, and 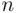 identical (indistinguishable) balls. In how many ways can these balls be distributed in
identical (indistinguishable) balls. In how many ways can these balls be distributed in 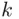 urns?
urns?
There are no restrictions here on the number of balls in an urn, or the number of empty urns. To get the answer, let us identify each possible allocation with a string of 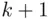 bars and
bars and 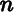 circles, of the form
circles, of the form
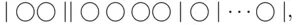
with the only condition being that the string should start and end with a bar. The spaces between bars represent urns. Thus, in the arrangement above, the first urn contains 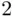 balls, the second none, the third 4 balls, and so on. Clearly, the number of distinct arrangements equals
balls, the second none, the third 4 balls, and so on. Clearly, the number of distinct arrangements equals 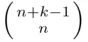 —the number of distinct arrangements of
—the number of distinct arrangements of  bars and
bars and 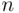 circles. Indeed, we have a string of
circles. Indeed, we have a string of 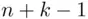 symbols (not counting the two extreme bars), and each arrangement is obtained by specifying
symbols (not counting the two extreme bars), and each arrangement is obtained by specifying 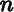 places for the symbol
places for the symbol  .
.
Example 3.10shows that the binomial coefficient can be interpreted in two ways. On the one hand, 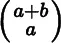 is the number
is the number 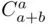 of distinct sets of size
of distinct sets of size 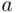 that can be chosen out of a set of size
that can be chosen out of a set of size 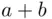 . On the other hand,
. On the other hand,  is also the number of distinct strings of
is also the number of distinct strings of 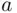 indistinguishable elements of one kind and
indistinguishable elements of one kind and 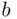 indistinguishable elements of another kind. To see this, it suffices to think of the string as being determined by the choice of “
indistinguishable elements of another kind. To see this, it suffices to think of the string as being determined by the choice of “ 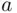 out of total of
out of total of 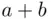 ” slots into which we assign elements of the first kind.
” slots into which we assign elements of the first kind.
Читать дальше

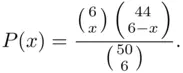
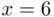 , we have
, we have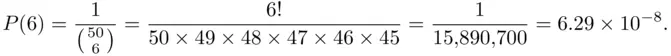
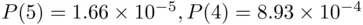 and
and 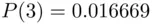 .
.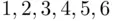 appears less likely than (say)
appears less likely than (say) 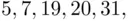 and 45. As a consequence some combinations are selected more often by the players than others. Each combination has the same chance of being the winning one, but some may have higher numbers of winners associated with them. This point can be illustrated by the following analogy: Imagine that each week a first name (Mary, Susan, George, etc.) is chosen at random from the set of all names used, and all persons in the state with the selected name share the prize. The chances of being chosen are the same for John as for Sebastian, as they depend on the process of sampling names of winners. But if the name Sebastian is chosen, each Sebastian will share the prize with many fewer other winners than if the name John were selected. Here the numbers of winners to share the prize depend on another process, namely that of parents selecting names for their children.
and 45. As a consequence some combinations are selected more often by the players than others. Each combination has the same chance of being the winning one, but some may have higher numbers of winners associated with them. This point can be illustrated by the following analogy: Imagine that each week a first name (Mary, Susan, George, etc.) is chosen at random from the set of all names used, and all persons in the state with the selected name share the prize. The chances of being chosen are the same for John as for Sebastian, as they depend on the process of sampling names of winners. But if the name Sebastian is chosen, each Sebastian will share the prize with many fewer other winners than if the name John were selected. Here the numbers of winners to share the prize depend on another process, namely that of parents selecting names for their children.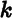 urns, labeled
urns, labeled  , and
, and 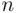 identical (indistinguishable) balls. In how many ways can these balls be distributed in
identical (indistinguishable) balls. In how many ways can these balls be distributed in 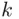 urns?
urns?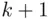 bars and
bars and 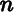 circles, of the form
circles, of the form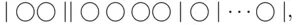
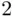 balls, the second none, the third 4 balls, and so on. Clearly, the number of distinct arrangements equals
balls, the second none, the third 4 balls, and so on. Clearly, the number of distinct arrangements equals 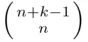 —the number of distinct arrangements of
—the number of distinct arrangements of  bars and
bars and 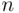 circles. Indeed, we have a string of
circles. Indeed, we have a string of 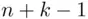 symbols (not counting the two extreme bars), and each arrangement is obtained by specifying
symbols (not counting the two extreme bars), and each arrangement is obtained by specifying 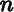 places for the symbol
places for the symbol 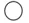 .
.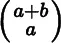 is the number
is the number 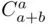 of distinct sets of size
of distinct sets of size 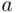 that can be chosen out of a set of size
that can be chosen out of a set of size 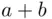 . On the other hand,
. On the other hand,  is also the number of distinct strings of
is also the number of distinct strings of 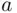 indistinguishable elements of one kind and
indistinguishable elements of one kind and 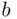 indistinguishable elements of another kind. To see this, it suffices to think of the string as being determined by the choice of “
indistinguishable elements of another kind. To see this, it suffices to think of the string as being determined by the choice of “ 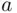 out of total of
out of total of 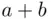 ” slots into which we assign elements of the first kind.
” slots into which we assign elements of the first kind.










