Robert Bartoszynski - Probability and Statistical Inference
Здесь есть возможность читать онлайн «Robert Bartoszynski - Probability and Statistical Inference» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Probability and Statistical Inference
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Probability and Statistical Inference: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Probability and Statistical Inference»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Probability and Statistical Inference, Third Edition
Probability and Statistical Inference

 be positive integers such that
be positive integers such that 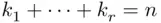 . The number of ways a set of
. The number of ways a set of 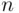 elements can be partitioned into
elements can be partitioned into 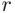 subsets of sizes
subsets of sizes  equals
equals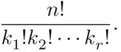
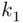 out of
out of 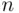 elements to form the first subset of the partition. Next, we choose
elements to form the first subset of the partition. Next, we choose 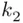 elements out of the remaining
elements out of the remaining 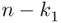 elements, and so on, until we have
elements, and so on, until we have 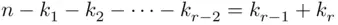 elements, from which we choose
elements, from which we choose 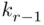 to form the next‐to‐last subset. The remaining
to form the next‐to‐last subset. The remaining 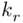 elements form the last subset This can be accomplished, in view of Theorem 3.2.2, in
elements form the last subset This can be accomplished, in view of Theorem 3.2.2, in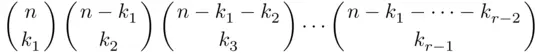
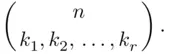
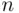 ,
,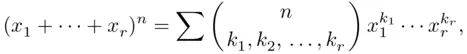
 of nonnegative integers with
of nonnegative integers with 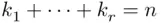 .
. , one term is taken from each factor so that the general term of the sum has the form
, one term is taken from each factor so that the general term of the sum has the form  with
with 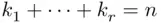 . From Theorem 3.4.1, it follows that the number of times the product
. From Theorem 3.4.1, it follows that the number of times the product  appears equals ( 3.26).
appears equals ( 3.26).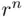 , which follows by substituting
, which follows by substituting 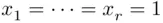 in ( 3.28).
in ( 3.28).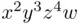 in the expression
in the expression 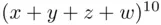 . One could argue that in the multiplication
. One could argue that in the multiplication  there are 10 factors, and each term will contain one component from each set of parentheses. Thus, choosing
there are 10 factors, and each term will contain one component from each set of parentheses. Thus, choosing 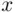 from 2 out of 10 pairs of parentheses,
from 2 out of 10 pairs of parentheses, 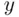 from 3 out of 10, and so on, amounts to partitioning 10 pairs of parentheses into four classes, with sizes
from 3 out of 10, and so on, amounts to partitioning 10 pairs of parentheses into four classes, with sizes 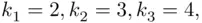 and
and 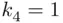 . The total number of ways such a partition can be accomplished is the coefficient of
. The total number of ways such a partition can be accomplished is the coefficient of 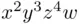 , and equals
, and equals 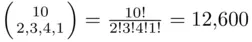 .
.










