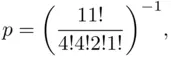
which is the same as ( 3.5).
Example 3.5 Birthday Problem
The following problem has a long tradition and appears in many textbooks. If 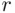 randomly chosen persons attend a party, what is the probability
randomly chosen persons attend a party, what is the probability 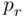 that none of them will have a birthday on the same day?
that none of them will have a birthday on the same day?
Here we make the following assumption: (1) all years have 365 days (i.e., leap years are disregarded), (2) each day is equally likely to be a birthday of a person (i.e., births occur uniformly throughout the year), and (3) no twins attend the party. To compute 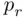 , we must find the number of all possible ways in which birthdays can be allocated to
, we must find the number of all possible ways in which birthdays can be allocated to 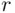 people, and the number of such allocations in which birthdays do not repeat. The first number is
people, and the number of such allocations in which birthdays do not repeat. The first number is 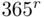 (by Theorem 3.2.3), while the second number is
(by Theorem 3.2.3), while the second number is 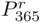 (assuming
(assuming 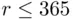 ; if
; if 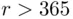 , we must have at least one birthday repeating, so
, we must have at least one birthday repeating, so 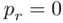 ). Thus, for
). Thus, for 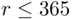 , we have
, we have
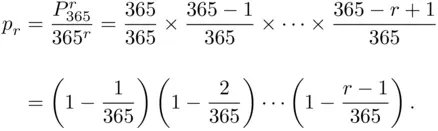
As a first approximation, neglecting all products which have denominators of order  or higher, we can take
or higher, we can take
(3.6) 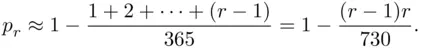
This approximation works quite well for small 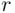 . Now since
. Now since 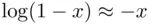 , we have
, we have
(3.7) 
It is interesting that for 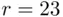 a repeated birthday is about as likely as no repetition. The smallest
a repeated birthday is about as likely as no repetition. The smallest 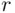 for which
for which 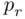 is less than 0.01 is 56.
is less than 0.01 is 56.
1 3.2.1 A certain set contains distinct elements. Find if the number of: (i) All possible permutations of length 2 equals 90. (ii) Permutations of length 3 is 10 times larger than the number of permutations of length 2.
2 3.2.2 A skyscraper is 40 stories tall. Five people enter the elevator on the first floor. Assuming each person is equally likely to get off at any of the 39 floors what is the probability that all people will get off at different floors? Find the exact value, and then derive and compute the approximations analogous to ( 3.6) and ( 3.7).
3 3.2.3 A two letter code is to be formed by selecting (without replacement) the letters from a given word. Find the number of possible codes if the word is: (i) CHART. (ii) ALOHA. (iii) STREET.
4 3.2.4 Determine the number of 0s at the end of 16! and 27!.
5 3.2.5 Seated at random in a row of seats are people, among them John and Mary. Find the probability that: (i) John sits next to Mary. (ii) John sits next to Mary on her right. (iii) John sits somewhere to the right of Mary. (iv) John and Mary sit exactly two seats apart.
6 3.2.6 Seated at random at a round table with seats are people, among them John and Mary. (i) Answer questions (i)–(iv) of Problem 3.2.5. Anything peculiar about the answer to (iii)? (ii) Assume that Find the probability that John and Mary sit facing each other (e.g., numbers 1 and 7 on the clock). (iii) Assume that . Find the probability that good friends, Nico, Noah, and Helen, are not separated by other guests.
7 3.2.7 Five men and five women are to be seated in a row of 10 chairs. Find the number of possible arrangements if: (i) Men are required to sit in alternating seats. (ii) No two men are to be seated next to each other.
8 3.2.8 A total of 12 girls and 17 boys go to a dance. (i) How many possible dancing pairs (boy–girl) may be formed? (ii) The dance floor can accommodate at most 11 pairs at a time. If each dance lasts 10 minutes and is followed by a 2‐minute break, how much time, at least, will elapse before each boy will have danced with each girl at least once? (iii) Answer the same question as in (ii) if the dance floor can accommodate 15 pairs at a time.
9 3.2.9 Susan has five dresses, three skirts, four blouses, three pairs of shoes, and two hats. She always wears shoes and either a dress or a blouse and a skirt. She may or may not wear a hat. (i) How many different combinations can she wear? (ii) Suppose Susan can afford buying either a dress or a hat (but not both). What should she buy to maximize the number of different combinations that she can wear? (iii) Suppose that Susan's brown shoes do not match her pink or blue dress and that the blue hat does not match her yellow blouse. How many matching combinations can she wear?
10 3.2.10 A restaurant menu has 5 appetizers, 3 soups, 15 entrees, and 3 desserts. (i) Assuming you are going to order one item from each group, how many possible dinners can you order? (ii) Assume you are at the restaurant with a friend. How many different orders for two full dinners can you place if your friend's choice of every item is not necessarily the same as yours? (iii) Answer the question in part (ii) under the constraint that you do not order the same entree and the same dessert as your friend (but the soup and/or appetizer may be the same).
11 3.2.11 Find the percentage of six‐digit numbers that have all digits distinct.
Читать дальше

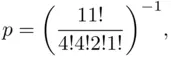
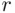 randomly chosen persons attend a party, what is the probability
randomly chosen persons attend a party, what is the probability 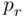 that none of them will have a birthday on the same day?
that none of them will have a birthday on the same day?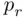 , we must find the number of all possible ways in which birthdays can be allocated to
, we must find the number of all possible ways in which birthdays can be allocated to 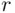 people, and the number of such allocations in which birthdays do not repeat. The first number is
people, and the number of such allocations in which birthdays do not repeat. The first number is 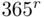 (by Theorem 3.2.3), while the second number is
(by Theorem 3.2.3), while the second number is 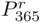 (assuming
(assuming 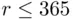 ; if
; if 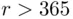 , we must have at least one birthday repeating, so
, we must have at least one birthday repeating, so 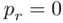 ). Thus, for
). Thus, for 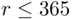 , we have
, we have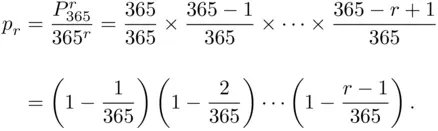
 or higher, we can take
or higher, we can take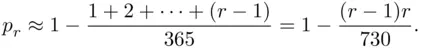
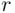 . Now since
. Now since 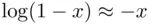 , we have
, we have
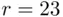 a repeated birthday is about as likely as no repetition. The smallest
a repeated birthday is about as likely as no repetition. The smallest 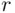 for which
for which 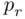 is less than 0.01 is 56.
is less than 0.01 is 56.










