Theorem 3.2.2allows for an immediate generalization, we can define Cartesian products of more than two sets. Thus, if  are some sets, then their Cartesian product
are some sets, then their Cartesian product 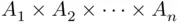 is the set of all
is the set of all  ‐tuples
‐tuples 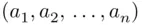 with
with 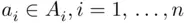 . By easy induction, Theorem 3.2.2can now be generalized as follows:
. By easy induction, Theorem 3.2.2can now be generalized as follows:
Theorem 3.2.3 If  are finite, with
are finite, with 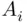 consisting of
consisting of 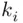 elements
elements  , then
, then  contains
contains  elements.
elements.
The total number of possible initials consisting of three letters (name, middle name, family name) is 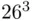 . Each three‐letter initial is an element of the set
. Each three‐letter initial is an element of the set 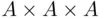 , where
, where 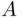 is the alphabet, so
is the alphabet, so 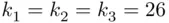 . The total number of possible two‐ or three‐letter initials is the number of the elements in the union
. The total number of possible two‐ or three‐letter initials is the number of the elements in the union 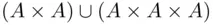 , equal to
, equal to 
Example 3.3 License Plates
Most states now use the system where a license plate has six symbols. One type (call it A) of such licenses has a prefix of three letters followed by a three‐digit number (e.g., CQX 786). Other states use system (call it B) with a two‐letter prefix, followed by a four‐digit number (e.g., KN 7207). Still other states use system C, a digit and two letters, followed by a three digit number (e.g., 2CP 412). In addition states allow (for a special fee) “personalized” plates such as CATHY3 or MYCAR. Disregarding the personalized plates, which type of the license plate system can register most cars?
Let 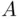 and
and 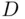 stand for the alphabet and for the set of 10 digits:
stand for the alphabet and for the set of 10 digits:  Then, a license plate from system A can be regarded as an element of
Then, a license plate from system A can be regarded as an element of 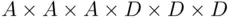 , while a license plate in system B is an element of the set
, while a license plate in system B is an element of the set 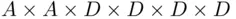 . The numbers of elements in these Cartesian products are
. The numbers of elements in these Cartesian products are  and
and 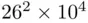 . The ratio is
. The ratio is 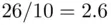 , so in the state using an A system 2.6 times more cars can be registered than in the state with a B system.
, so in the state using an A system 2.6 times more cars can be registered than in the state with a B system.
Regarding system C, the answer depends whether or not 0 is allowed in the prefix. If the plate such as 0HY 314 is not allowed (e.g., because the digit 0 can be confused with the letter O), then the number of possible license plates is only 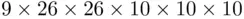 , which is 10% less than the number of plates possible in states using system B. If 0 is allowed as the first character, then the numbers of plates of types
, which is 10% less than the number of plates possible in states using system B. If 0 is allowed as the first character, then the numbers of plates of types 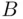 and
and 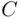 are the same.
are the same.
In Examples 3.1through 3.3the set of ways of performing the second operations is the same regardless of which option was selected for the first operation. However, Theorem 3.2.1remains true if the sets of ways of performing the second operation depend on the choice of the first operation. In particular, we can think of the first and second operation as two consecutive choices of an element from the same set , without returning the chosen elements. If the set, say 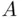 , has
, has 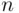 elements, then the first operation (choice of an element) can be performed in
elements, then the first operation (choice of an element) can be performed in 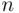 ways. If the chosen element is not returned, then the second choice can be performed in
ways. If the chosen element is not returned, then the second choice can be performed in  ways only, and we have the following:
ways only, and we have the following:
Читать дальше

 are some sets, then their Cartesian product
are some sets, then their Cartesian product 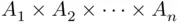 is the set of all
is the set of all  ‐tuples
‐tuples 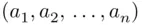 with
with 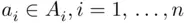 . By easy induction, Theorem 3.2.2can now be generalized as follows:
. By easy induction, Theorem 3.2.2can now be generalized as follows: are finite, with
are finite, with 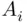 consisting of
consisting of 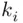 elements
elements  , then
, then  contains
contains  elements.
elements.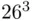 . Each three‐letter initial is an element of the set
. Each three‐letter initial is an element of the set 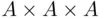 , where
, where 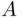 is the alphabet, so
is the alphabet, so 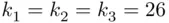 . The total number of possible two‐ or three‐letter initials is the number of the elements in the union
. The total number of possible two‐ or three‐letter initials is the number of the elements in the union 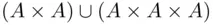 , equal to
, equal to 
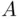 and
and 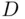 stand for the alphabet and for the set of 10 digits:
stand for the alphabet and for the set of 10 digits:  Then, a license plate from system A can be regarded as an element of
Then, a license plate from system A can be regarded as an element of 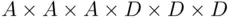 , while a license plate in system B is an element of the set
, while a license plate in system B is an element of the set 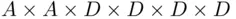 . The numbers of elements in these Cartesian products are
. The numbers of elements in these Cartesian products are  and
and 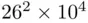 . The ratio is
. The ratio is 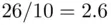 , so in the state using an A system 2.6 times more cars can be registered than in the state with a B system.
, so in the state using an A system 2.6 times more cars can be registered than in the state with a B system.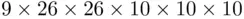 , which is 10% less than the number of plates possible in states using system B. If 0 is allowed as the first character, then the numbers of plates of types
, which is 10% less than the number of plates possible in states using system B. If 0 is allowed as the first character, then the numbers of plates of types 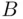 and
and 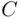 are the same.
are the same.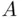 , has
, has 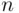 elements, then the first operation (choice of an element) can be performed in
elements, then the first operation (choice of an element) can be performed in 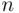 ways. If the chosen element is not returned, then the second choice can be performed in
ways. If the chosen element is not returned, then the second choice can be performed in  ways only, and we have the following:
ways only, and we have the following:










