This scheme of measurement may provide an assessment of the values of the (subjective) probabilities of a given person, for a class of events. It is of considerable interest that the same scheme was suggested in 1944 by von Neumann and Morgenstern (1944) as a tool for measuring utilities. They assumed that probabilities are known (i.e., the person whose utility is being assessed knows the objective probabilities of events, and his subjective and objective probabilities coincide). If a person is now indifferent between the lottery as above, and the sure option of receiving an object, say 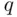 , then the utility
, then the utility  of object
of object 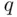 must equal the expected value of the lottery, which is
must equal the expected value of the lottery, which is 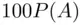 . This allows one to measure utilities on the scale that has a zero set on nothing (status quo) and “unit” as the utility of $100. The scheme of von Neumann and Morgenstern was later improved by some authors, culminating with the theorem of Blackwell and Girshick (1954).
. This allows one to measure utilities on the scale that has a zero set on nothing (status quo) and “unit” as the utility of $100. The scheme of von Neumann and Morgenstern was later improved by some authors, culminating with the theorem of Blackwell and Girshick (1954).
Still the disadvantages of both approaches were due to the fact that to determine utilities, one needed to assume knowledge of probabilities by the subject, while conversely, to determine subjective probabilities, one needed to assume knowledge of utilities. The discovery that one can determine both utilities and subjective probabilities of the same person is due to Savage (1954). We present here the basic idea of the experiment rather than formal axioms (to avoid obscuring the issue by technicalities).
Let 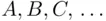 denote events, and let
denote events, and let 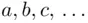 denote some objects, whose probabilities
denote some objects, whose probabilities 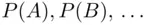 and utilities
and utilities 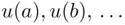 are to be determined (keep in mind that both
are to be determined (keep in mind that both 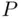 and
and 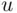 refer to a particular person X, the subject of the experiment). We now accept the main postulate of the theory, that of the two lotteries, X will prefer the one that has higher SEU.
refer to a particular person X, the subject of the experiment). We now accept the main postulate of the theory, that of the two lotteries, X will prefer the one that has higher SEU.
Suppose that we find an event 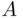 with subjective probability
with subjective probability 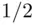 , so that
, so that 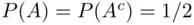 . If X prefers lottery
. If X prefers lottery 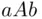 to lottery
to lottery 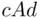 , then
, then
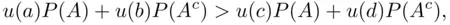
which means that
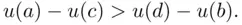
A number of experiments on selected objects will allow us to estimate the utilities, potentially with an arbitrary accuracy (taking two particular objects as zero and a unit of the utility scale). In turn, if we know the utilities, we can determine the subjective probability of any event 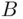 . That is, if X is indifferent between lotteries
. That is, if X is indifferent between lotteries 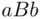 and
and 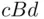 , we have
, we have
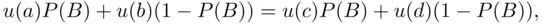
which gives
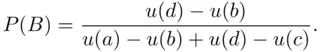
The only problem lies in finding an event 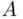 with subjective probability
with subjective probability 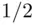 . Empirically, an event
. Empirically, an event 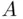 has subjective probability
has subjective probability 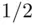 if, for any objects
if, for any objects 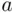 and
and 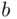 , the person is indifferent between lotteries
, the person is indifferent between lotteries 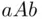 and
and 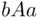 . Such an event was found experimentally (Davidson et al., 1957). It is related to a toss of a die with three of the faces marked with the nonsense combination
. Such an event was found experimentally (Davidson et al., 1957). It is related to a toss of a die with three of the faces marked with the nonsense combination 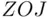 , and the other three with the nonsense combination
, and the other three with the nonsense combination 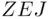 (these combinations evoked the least number of associations).
(these combinations evoked the least number of associations).
Let us remark at this point that the system of Savage involves determining first an event with probability 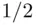 , then the utilities, and then the subjective probabilities. Luce and Krantz (1971) suggested an axiom system (leading to an appropriate scheme) that allows simultaneous determination of utilities and probabilities. The reader interested in these topics is referred to the monograph by Krantz et al. (1971).
, then the utilities, and then the subjective probabilities. Luce and Krantz (1971) suggested an axiom system (leading to an appropriate scheme) that allows simultaneous determination of utilities and probabilities. The reader interested in these topics is referred to the monograph by Krantz et al. (1971).
Читать дальше

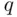 , then the utility
, then the utility  of object
of object 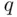 must equal the expected value of the lottery, which is
must equal the expected value of the lottery, which is 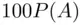 . This allows one to measure utilities on the scale that has a zero set on nothing (status quo) and “unit” as the utility of $100. The scheme of von Neumann and Morgenstern was later improved by some authors, culminating with the theorem of Blackwell and Girshick (1954).
. This allows one to measure utilities on the scale that has a zero set on nothing (status quo) and “unit” as the utility of $100. The scheme of von Neumann and Morgenstern was later improved by some authors, culminating with the theorem of Blackwell and Girshick (1954).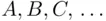 denote events, and let
denote events, and let 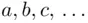 denote some objects, whose probabilities
denote some objects, whose probabilities 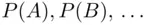 and utilities
and utilities 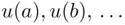 are to be determined (keep in mind that both
are to be determined (keep in mind that both 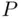 and
and 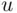 refer to a particular person X, the subject of the experiment). We now accept the main postulate of the theory, that of the two lotteries, X will prefer the one that has higher SEU.
refer to a particular person X, the subject of the experiment). We now accept the main postulate of the theory, that of the two lotteries, X will prefer the one that has higher SEU.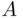 with subjective probability
with subjective probability 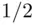 , so that
, so that 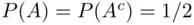 . If X prefers lottery
. If X prefers lottery 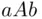 to lottery
to lottery 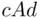 , then
, then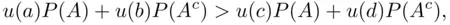
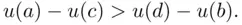
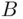 . That is, if X is indifferent between lotteries
. That is, if X is indifferent between lotteries 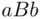 and
and 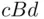 , we have
, we have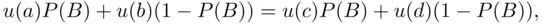
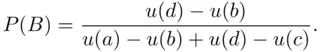
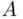 with subjective probability
with subjective probability 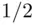 . Empirically, an event
. Empirically, an event 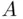 has subjective probability
has subjective probability 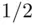 if, for any objects
if, for any objects 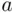 and
and 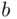 , the person is indifferent between lotteries
, the person is indifferent between lotteries 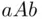 and
and 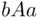 . Such an event was found experimentally (Davidson et al., 1957). It is related to a toss of a die with three of the faces marked with the nonsense combination
. Such an event was found experimentally (Davidson et al., 1957). It is related to a toss of a die with three of the faces marked with the nonsense combination 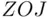 , and the other three with the nonsense combination
, and the other three with the nonsense combination 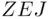 (these combinations evoked the least number of associations).
(these combinations evoked the least number of associations).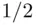 , then the utilities, and then the subjective probabilities. Luce and Krantz (1971) suggested an axiom system (leading to an appropriate scheme) that allows simultaneous determination of utilities and probabilities. The reader interested in these topics is referred to the monograph by Krantz et al. (1971).
, then the utilities, and then the subjective probabilities. Luce and Krantz (1971) suggested an axiom system (leading to an appropriate scheme) that allows simultaneous determination of utilities and probabilities. The reader interested in these topics is referred to the monograph by Krantz et al. (1971).










