2.7 Subjective Probability*
Let us finally consider briefly the third interpretation of probability, namely as a degree of certainty, or belief, about the occurrence of an event. Most often, this probability is associated not so much with an event as with the truth of a proposition asserting the occurrence of this event.
The material of this section assumes some degree of familiarity with the concept of expectation, formally defined only in later chapters. For the sake of completeness, in the simple form needed here, this concept is defined below. In the presentation, we follow more or less the historical development, refining gradually the conceptual structures introduced. The basic concept here is that of a lottery , defined by an event, say 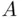 , and two objects, say
, and two objects, say 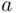 and
and 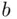 . Such a lottery, written simply
. Such a lottery, written simply 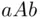 , will mean that the participant (X) in the lottery receives object
, will mean that the participant (X) in the lottery receives object 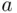 if the event
if the event 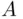 occurs, and receives object
occurs, and receives object 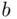 if the event
if the event 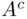 occurs.
occurs.
The second concept is that of expectation associated with the lottery 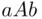 , defined as
, defined as
(2.13) 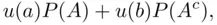
where 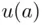 and
and 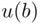 are measures of how much the objects
are measures of how much the objects  and
and 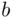 are “worth” to the participant. When
are “worth” to the participant. When 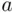 and
and  are sums of money (or prices of objects
are sums of money (or prices of objects 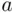 and
and 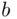 ), and we put
), and we put 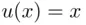 , the quantity ( 2.13) is sometimes called expected value . In cases where
, the quantity ( 2.13) is sometimes called expected value . In cases where 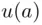 and
and 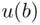 are values that person X attaches to
are values that person X attaches to 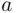 and
and 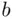 (at a given moment), these values do not necessarily coincide with prices. We then refer to
(at a given moment), these values do not necessarily coincide with prices. We then refer to 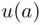 and
and 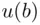 as utilities of
as utilities of 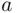 and
and 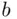 , and the quantity ( 2.13) is called expected utility ( EU ). Finally, when in the latter case, the probability
, and the quantity ( 2.13) is called expected utility ( EU ). Finally, when in the latter case, the probability 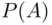 is the subjective assessment of likelihood of the event
is the subjective assessment of likelihood of the event 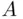 by X, the quantity ( 2.13) is called subjective expected utility ( SEU ).
by X, the quantity ( 2.13) is called subjective expected utility ( SEU ).
First, it has been shown by Ramsey (1926) that the degree of certainty about the occurrence of an event (of a given person) can be measured. Consider an event 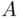 , and the following choice suggested to X (whose subjective probability we want to determine). X is namely given a choice between the following two options:
, and the following choice suggested to X (whose subjective probability we want to determine). X is namely given a choice between the following two options:
1 Sure option: receive some fixed amount , which is the same as lottery , for any event .
2 A lottery option. Receive some fixed amount, say $100, if occurs, and receive nothing if does not occur, which is lottery . One should expect that if is very small, X will probably prefer the lottery. On the other hand, if is close to , X may prefer the sure option.
Therefore, there should exist an amount 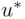 such that X will be indifferent between the sure option with
such that X will be indifferent between the sure option with 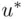 and the lottery option. With the amount of money as a representation of its value (or utility), the expected return from the lottery equals
and the lottery option. With the amount of money as a representation of its value (or utility), the expected return from the lottery equals
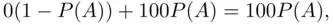
which, in turn, equals 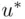 . Consequently, we have
. Consequently, we have 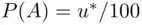 . Obviously, under the stated assumption that utility of money is proportional to the dollar amount, the choice of
. Obviously, under the stated assumption that utility of money is proportional to the dollar amount, the choice of 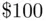 is not relevant here, and the same value for
is not relevant here, and the same value for 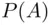 would be obtained if we choose another “base value” in the lottery option (this can be tested empirically).
would be obtained if we choose another “base value” in the lottery option (this can be tested empirically).
Читать дальше

 , and two objects, say
, and two objects, say 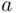 and
and 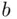 . Such a lottery, written simply
. Such a lottery, written simply 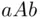 , will mean that the participant (X) in the lottery receives object
, will mean that the participant (X) in the lottery receives object 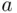 if the event
if the event 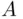 occurs, and receives object
occurs, and receives object 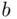 if the event
if the event 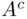 occurs.
occurs.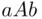 , defined as
, defined as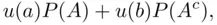
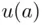 and
and 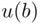 are measures of how much the objects
are measures of how much the objects  and
and 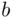 are “worth” to the participant. When
are “worth” to the participant. When 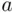 and
and  are sums of money (or prices of objects
are sums of money (or prices of objects 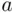 and
and 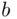 ), and we put
), and we put 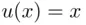 , the quantity ( 2.13) is sometimes called expected value . In cases where
, the quantity ( 2.13) is sometimes called expected value . In cases where 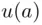 and
and 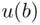 are values that person X attaches to
are values that person X attaches to 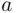 and
and 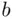 (at a given moment), these values do not necessarily coincide with prices. We then refer to
(at a given moment), these values do not necessarily coincide with prices. We then refer to 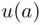 and
and 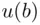 as utilities of
as utilities of 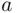 and
and 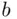 , and the quantity ( 2.13) is called expected utility ( EU ). Finally, when in the latter case, the probability
, and the quantity ( 2.13) is called expected utility ( EU ). Finally, when in the latter case, the probability 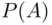 is the subjective assessment of likelihood of the event
is the subjective assessment of likelihood of the event 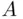 by X, the quantity ( 2.13) is called subjective expected utility ( SEU ).
by X, the quantity ( 2.13) is called subjective expected utility ( SEU ).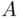 , and the following choice suggested to X (whose subjective probability we want to determine). X is namely given a choice between the following two options:
, and the following choice suggested to X (whose subjective probability we want to determine). X is namely given a choice between the following two options: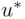 such that X will be indifferent between the sure option with
such that X will be indifferent between the sure option with 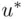 and the lottery option. With the amount of money as a representation of its value (or utility), the expected return from the lottery equals
and the lottery option. With the amount of money as a representation of its value (or utility), the expected return from the lottery equals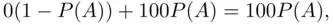
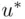 . Consequently, we have
. Consequently, we have 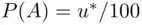 . Obviously, under the stated assumption that utility of money is proportional to the dollar amount, the choice of
. Obviously, under the stated assumption that utility of money is proportional to the dollar amount, the choice of 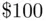 is not relevant here, and the same value for
is not relevant here, and the same value for 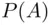 would be obtained if we choose another “base value” in the lottery option (this can be tested empirically).
would be obtained if we choose another “base value” in the lottery option (this can be tested empirically).










