Robert Bartoszynski - Probability and Statistical Inference

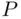A comment that is necessary here concerns the question: What does it mean that a function defined on a field 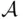satisfies the axioms of probability? Specifically, the problem concerns the axiom of countable additivity, which asserts that if events are disjoint, then

(2.11)

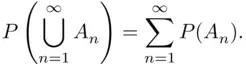
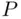However, if is defined on a field, then there is no guarantee that the left‐hand side of formula ( (2.11)) makes sense, since 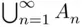need not belong to the field of events on which is defined. The meaning of the assumption of Theorem 2.6.3is that formula ( 2.11) is true whenever the union 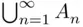belongs to the field on which is defined.

The way of finding the probability of some complicated event is to represent 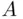as a limit of some sequence of events whose probabilities can be computed, and then pass to the limit. Theorem 2.6.3asserts that this procedure will give the same result, regardless of the choice of sequence of events approximating the event .

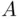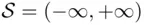A very common situation in probability theory occurs when . A probability measure 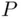on 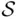can be defined as follows: let 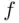be a function such that 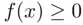for all 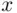and 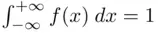. We will assume in addition that 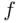is continuous and bounded, although those conditions can be greatly relaxed in general theory.

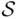We now define probability on by putting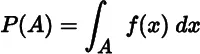

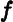(2.12)

(in this case, is referred to as a density of 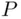). The full justification of this construction lies beyond the scope of this book, but we will give the main points. First, the definition ( 2.12) is applicable for all intervals 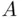of the form 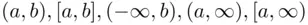, and so on. Then we can extend to finite unions of disjoint intervals by additivity (the class of all such finite unions forms a field). We can easily check that such an extension is unique; that is,

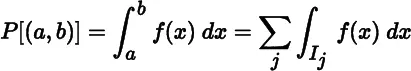
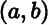does not depend on the way interval is partitioned into the finite union of nonoverlapping intervals 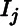. This provides an extension of 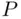to the smallest field of sets containing all intervals. If we show that 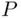defined this way is continuous on the empty set, then we can claim that there exists an extension of 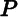to the smallest ‐field of sets containing all intervals.

Now, the decreasing sequences of intervals converging to the empty set are built of two kinds of sequences: “shrinking open sets” and “escaping sets,” exemplified as

and

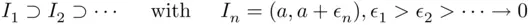
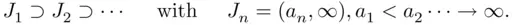
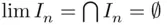We have here and 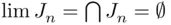. In the first case, 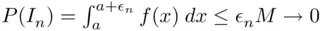, where 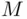is a bound for function 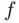. In the second case, .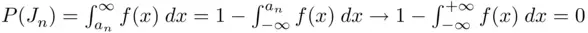