Either Paul tosses more heads than Peter (event 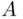 ) or he tosses more tails than Peter (event
) or he tosses more tails than Peter (event 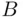 ). These two events exclude one another and exhaust all possibilities (since one cannot have ties in number of heads and number of tails). Switching the role of heads and tails transforms one of these events into the other. Thus, sample space becomes partitioned into two equiprobable events, and we must have
). These two events exclude one another and exhaust all possibilities (since one cannot have ties in number of heads and number of tails). Switching the role of heads and tails transforms one of these events into the other. Thus, sample space becomes partitioned into two equiprobable events, and we must have 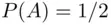 .
.
The use of ( 2.7) requires techniques for counting the numbers of elements in some sets. These topics, known under the name combinatorics , will be discussed in Chapter 3.
1 2.5.1 A coin is tossed seven times. Assume that each of the possible outcomes (sequences like HTTHHTH of length 7) is equally likely. Relate each outcome to a binary number by replacing H by 1 and T by 0, for example, THHHTTH is 0111001 = 57. Find the probability that a number generated in this way lies between 64 and 95 (inclusive on both sides).
2 2.5.2 A number is chosen at random from the series 4, 9, 14, 19, …, and another number is chosen from the series 1, 5, 9, 13, …. Each series has 100 terms. Find .
3 2.5.3 A regular die and a die with 2, 3, 5, 6, 7, and 8 dots are tossed together, and the total number of dots is noted. What is the probability that the sum is greater than or equal to 10?
4 2.5.4 Use formula ( 2.6) to find the number of primes not exceeding 100. [Hint: Assume that you sample one of the numbers 1, 2, …, 100. Let be the event “the number sampled is divisible by .” Determine . Then the answer to the problem is (why?).]
2.6 Necessity of the Axioms*
Looking at Axiom 3, one may wonder why do we need it for the case of countable (and not just finite) sequences of events. Indeed, the necessity of all three axioms, with only finite additivity in Axiom 3, can be easily justified simply by using probability to represent the limiting relative frequency of occurrences of events. Recall the symbol 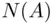 from Section 2.1for the number of occurrences of the event
from Section 2.1for the number of occurrences of the event 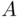 in the first
in the first 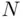 experiments. The nonnegativity axiom is simply a reflection of the fact that the count
experiments. The nonnegativity axiom is simply a reflection of the fact that the count 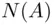 cannot be negative. The norming axiom reflects the fact that event
cannot be negative. The norming axiom reflects the fact that event 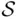 is certain and must occur in every experiment so that
is certain and must occur in every experiment so that 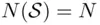 , and hence,
, and hence, 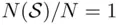 . Finally, (taking the case of two disjoint events
. Finally, (taking the case of two disjoint events  and
and 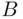 ), we have
), we have 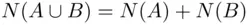 , since whenever
, since whenever 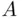 occurs,
occurs, 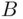 does not, and conversely. Thus, if probability is to reflect the limiting relative frequency, then
does not, and conversely. Thus, if probability is to reflect the limiting relative frequency, then 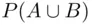 should be equal to
should be equal to 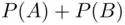 , since the frequencies satisfy the analogous condition
, since the frequencies satisfy the analogous condition 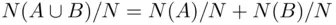 .
.
The need for countable additivity, however, cannot be explained so simply. This need is related to the fact that to build a sufficiently powerful theory, one needs to take limits. If 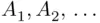 is a monotone sequence of events (increasing or decreasing, i.e.,
is a monotone sequence of events (increasing or decreasing, i.e., 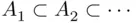 or
or 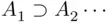 ) then
) then 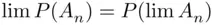 , where the event
, where the event 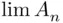 has been defined in Section 1.4. Upon a little reflection, one can see that such continuity is a very natural requirement. In fact, the same requirement has been taken for granted for over 2,000 years in a somewhat different context: in computing the area of a circle, one uses a sequence of polygons with an increasing number of sides, all inscribed in the circle. This leads to an increasing sequence of sets “converging” to the circle, and therefore the area of the circle is taken to be the limit of the areas of approximating polygons. The validity of this idea (i.e., the assumption of the continuity of the function
has been defined in Section 1.4. Upon a little reflection, one can see that such continuity is a very natural requirement. In fact, the same requirement has been taken for granted for over 2,000 years in a somewhat different context: in computing the area of a circle, one uses a sequence of polygons with an increasing number of sides, all inscribed in the circle. This leads to an increasing sequence of sets “converging” to the circle, and therefore the area of the circle is taken to be the limit of the areas of approximating polygons. The validity of this idea (i.e., the assumption of the continuity of the function 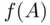 = area of
= area of 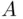 ) was not really questioned until the beginning of the twentieth century. Research on the subject culminated with the results of Lebesgue.
) was not really questioned until the beginning of the twentieth century. Research on the subject culminated with the results of Lebesgue.
To quote the relevant theorem, let us say that a function 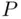 , defined on a class of sets (events), is continuous from below at the set
, defined on a class of sets (events), is continuous from below at the set 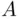 if the conditions
if the conditions 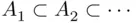 and
and 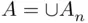 imply that
imply that 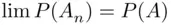 . Similarly,
. Similarly, 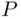 is continuous from above at the set
is continuous from above at the set 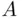 if the conditions
if the conditions 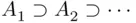 and
and 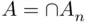 imply
imply 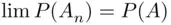 . A function that is continuous at every set from above or from below is simply called continuous (above or below). Continuity from below and from above is simply referred to as continuity .
. A function that is continuous at every set from above or from below is simply called continuous (above or below). Continuity from below and from above is simply referred to as continuity .
Читать дальше

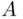 ) or he tosses more tails than Peter (event
) or he tosses more tails than Peter (event 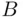 ). These two events exclude one another and exhaust all possibilities (since one cannot have ties in number of heads and number of tails). Switching the role of heads and tails transforms one of these events into the other. Thus, sample space becomes partitioned into two equiprobable events, and we must have
). These two events exclude one another and exhaust all possibilities (since one cannot have ties in number of heads and number of tails). Switching the role of heads and tails transforms one of these events into the other. Thus, sample space becomes partitioned into two equiprobable events, and we must have 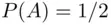 .
.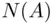 from Section 2.1for the number of occurrences of the event
from Section 2.1for the number of occurrences of the event 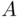 in the first
in the first 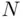 experiments. The nonnegativity axiom is simply a reflection of the fact that the count
experiments. The nonnegativity axiom is simply a reflection of the fact that the count 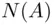 cannot be negative. The norming axiom reflects the fact that event
cannot be negative. The norming axiom reflects the fact that event 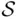 is certain and must occur in every experiment so that
is certain and must occur in every experiment so that 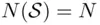 , and hence,
, and hence, 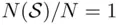 . Finally, (taking the case of two disjoint events
. Finally, (taking the case of two disjoint events  and
and 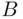 ), we have
), we have 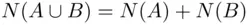 , since whenever
, since whenever 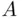 occurs,
occurs, 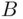 does not, and conversely. Thus, if probability is to reflect the limiting relative frequency, then
does not, and conversely. Thus, if probability is to reflect the limiting relative frequency, then 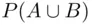 should be equal to
should be equal to 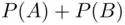 , since the frequencies satisfy the analogous condition
, since the frequencies satisfy the analogous condition 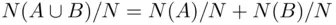 .
.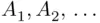 is a monotone sequence of events (increasing or decreasing, i.e.,
is a monotone sequence of events (increasing or decreasing, i.e., 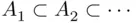 or
or 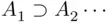 ) then
) then 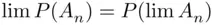 , where the event
, where the event 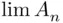 has been defined in Section 1.4. Upon a little reflection, one can see that such continuity is a very natural requirement. In fact, the same requirement has been taken for granted for over 2,000 years in a somewhat different context: in computing the area of a circle, one uses a sequence of polygons with an increasing number of sides, all inscribed in the circle. This leads to an increasing sequence of sets “converging” to the circle, and therefore the area of the circle is taken to be the limit of the areas of approximating polygons. The validity of this idea (i.e., the assumption of the continuity of the function
has been defined in Section 1.4. Upon a little reflection, one can see that such continuity is a very natural requirement. In fact, the same requirement has been taken for granted for over 2,000 years in a somewhat different context: in computing the area of a circle, one uses a sequence of polygons with an increasing number of sides, all inscribed in the circle. This leads to an increasing sequence of sets “converging” to the circle, and therefore the area of the circle is taken to be the limit of the areas of approximating polygons. The validity of this idea (i.e., the assumption of the continuity of the function 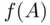 = area of
= area of 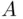 ) was not really questioned until the beginning of the twentieth century. Research on the subject culminated with the results of Lebesgue.
) was not really questioned until the beginning of the twentieth century. Research on the subject culminated with the results of Lebesgue.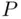 , defined on a class of sets (events), is continuous from below at the set
, defined on a class of sets (events), is continuous from below at the set 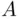 if the conditions
if the conditions 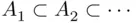 and
and 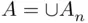 imply that
imply that 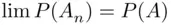 . Similarly,
. Similarly, 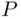 is continuous from above at the set
is continuous from above at the set 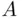 if the conditions
if the conditions 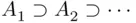 and
and 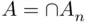 imply
imply 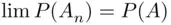 . A function that is continuous at every set from above or from below is simply called continuous (above or below). Continuity from below and from above is simply referred to as continuity .
. A function that is continuous at every set from above or from below is simply called continuous (above or below). Continuity from below and from above is simply referred to as continuity .










