From Figure 2.1, it is clear that the point of hit must lie somewhere in the shaded annulus 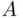 . Its area is
. Its area is 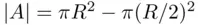 so that
so that 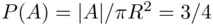 . Of course, the assumption under which this solution is obtained is not very realistic: typically sets closer to the center are more likely to be hit than sets of the same area located closer to the perimeter.
. Of course, the assumption under which this solution is obtained is not very realistic: typically sets closer to the center are more likely to be hit than sets of the same area located closer to the perimeter.
The concept of “random choice” from an uncountable set is sometimes ambiguous. This is illustrated by the next example.
Example 2.2 Bertrand's Paradox
A chord is chosen at random in a circle. What is the probability that the length of the chord will exceed the length of the side of an equilateral triangle inscribed in the circle?
This problem was originally posed in 1888 by Joseph Bertrand, a French mathematician, who provided three solutions, all valid, but yielding inconsistent results.
The chord is uniquely determined by the angle 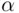 (see Figure 2.2). These angles are chosen at random from the interval
(see Figure 2.2). These angles are chosen at random from the interval 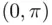 . It is clear that the length of the chord exceeds the side of the equilateral triangle if
. It is clear that the length of the chord exceeds the side of the equilateral triangle if 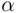 lies between
lies between 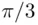 and
and 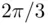 , so the answer to the question is
, so the answer to the question is  .
.
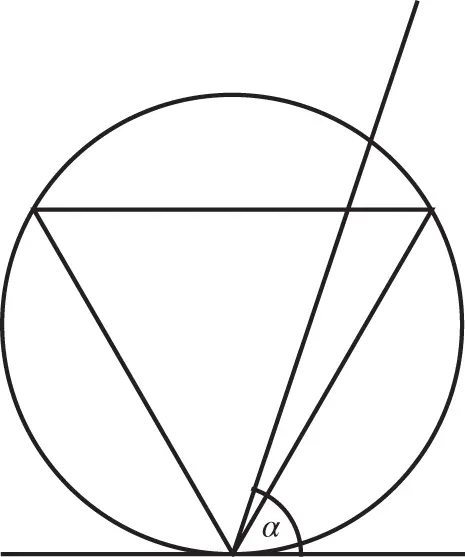
Figure 2.2First solution of Bertrand's problem.
Let us draw a diameter 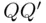 (see Figure 2.3) perpendicular to the chord
(see Figure 2.3) perpendicular to the chord 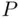 . Then, the length of the chord exceeds the side of the equilateral triangle if it intersects the line
. Then, the length of the chord exceeds the side of the equilateral triangle if it intersects the line 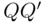 between points
between points 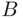 and
and 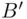 . Elementary calculations give
. Elementary calculations give 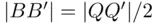 , so the answer is
, so the answer is 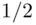 .
.
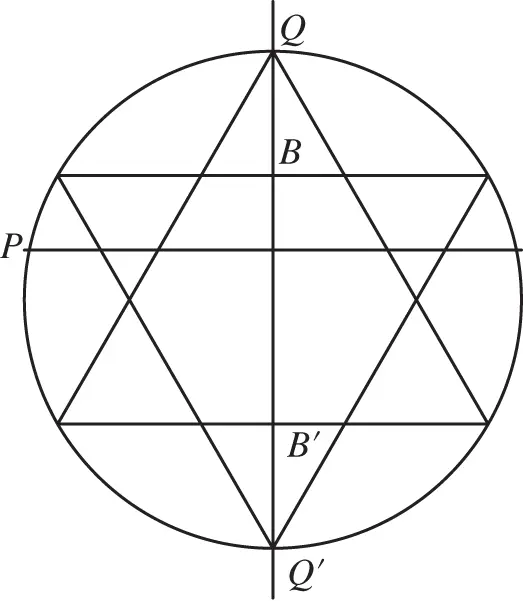
Figure 2.3Second solution of Bertrand's problem.
The location of the chord is uniquely determined by the location of its center (except when the center coincides with the center of the circle, which is an event with probability zero). For the chord to be longer than the side of the equilateral triangle inscribed in the circle, its center must fall somewhere inside the shaded circle in Figure 2.4. Again, by elementary calculations, we obtain probability 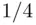 .
.
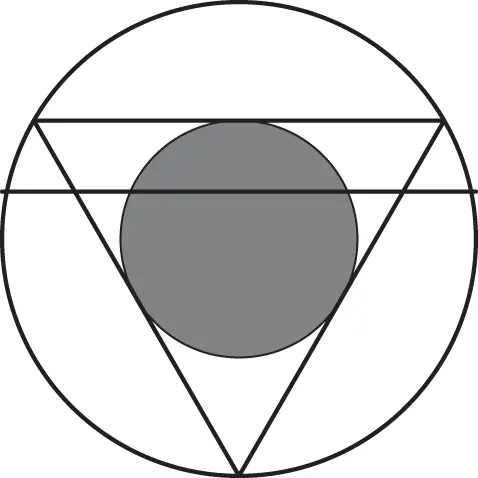
Figure 2.4Third solution of Bertrand's problem.
The discovery of Bertrand's paradox was one of the impulses that made researchers in probability and statistics acutely aware of the need to clarify the foundations of the theory, and ultimately led to the publication of Kolmogorov's book (1933). In the particular instance of the Bertrand “paradoxes,” they are explained simply by the fact that each of the solutions refers to a different sampling scheme: (1) choosing a point on the circumference and then choosing the angle between the chord and the tangent at the point selected, (2) choosing a diameter perpendicular to the chord and then selecting the point of intersection of the chord with this diameter, and (3) choosing a center of the chord. Random choice according to one of these schemes is not equivalent to a random choice according to the other two schemes.
To see why it is so, we will show that the first and second scheme are not equivalent. The analogous arguments for the other two possible pairs of schemes are left as an exercise.
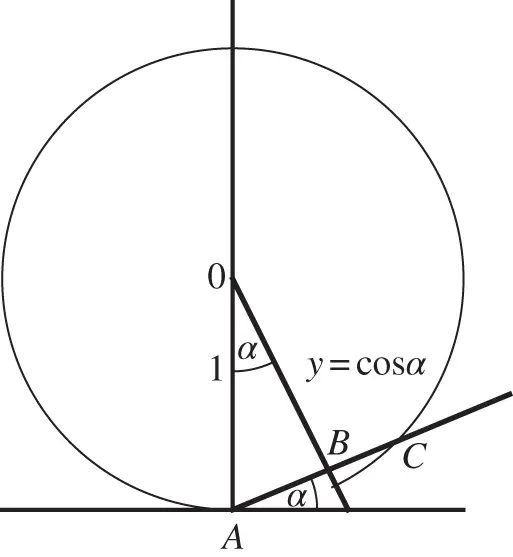
Figure 2.5Explanation of Bertrand's paradox.
Imagine different devices (physical mechanisms, computer programs, etc.) built for sampling random chords. One scheme chooses a point on the circumference, and then the angle  between the chord and the tangent to the circle at the point chosen ( Figure 2.2). The second scheme chooses first the direction of the diameter and then the point
between the chord and the tangent to the circle at the point chosen ( Figure 2.2). The second scheme chooses first the direction of the diameter and then the point 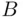 on the diameter, at which the chord perpendicular to this diameter intersects it ( Figure 2.3). From Figure 2.5, it is seen that the angle
on the diameter, at which the chord perpendicular to this diameter intersects it ( Figure 2.3). From Figure 2.5, it is seen that the angle 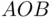 is
is 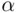 , and therefore
, and therefore 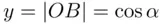 . Thus,
. Thus, 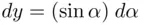 , which means that equal changes of
, which means that equal changes of 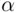 do not produce equal changes of
do not produce equal changes of 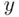 . In fact, these changes are smaller when
. In fact, these changes are smaller when 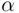 is small. Consequently, a device that chooses angles
is small. Consequently, a device that chooses angles  at random will tend to produce more intersections of the diameter that are farther from the center (i.e., more chords will be shorter).
at random will tend to produce more intersections of the diameter that are farther from the center (i.e., more chords will be shorter).
Читать дальше

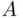 . Its area is
. Its area is 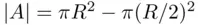 so that
so that 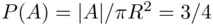 . Of course, the assumption under which this solution is obtained is not very realistic: typically sets closer to the center are more likely to be hit than sets of the same area located closer to the perimeter.
. Of course, the assumption under which this solution is obtained is not very realistic: typically sets closer to the center are more likely to be hit than sets of the same area located closer to the perimeter.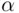 (see Figure 2.2). These angles are chosen at random from the interval
(see Figure 2.2). These angles are chosen at random from the interval 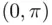 . It is clear that the length of the chord exceeds the side of the equilateral triangle if
. It is clear that the length of the chord exceeds the side of the equilateral triangle if 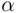 lies between
lies between 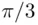 and
and 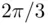 , so the answer to the question is
, so the answer to the question is  .
.
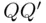 (see Figure 2.3) perpendicular to the chord
(see Figure 2.3) perpendicular to the chord 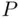 . Then, the length of the chord exceeds the side of the equilateral triangle if it intersects the line
. Then, the length of the chord exceeds the side of the equilateral triangle if it intersects the line 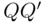 between points
between points 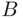 and
and 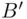 . Elementary calculations give
. Elementary calculations give 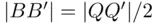 , so the answer is
, so the answer is 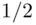 .
.
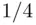 .
.

 between the chord and the tangent to the circle at the point chosen ( Figure 2.2). The second scheme chooses first the direction of the diameter and then the point
between the chord and the tangent to the circle at the point chosen ( Figure 2.2). The second scheme chooses first the direction of the diameter and then the point 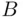 on the diameter, at which the chord perpendicular to this diameter intersects it ( Figure 2.3). From Figure 2.5, it is seen that the angle
on the diameter, at which the chord perpendicular to this diameter intersects it ( Figure 2.3). From Figure 2.5, it is seen that the angle 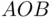 is
is 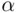 , and therefore
, and therefore 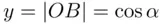 . Thus,
. Thus, 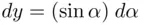 , which means that equal changes of
, which means that equal changes of 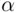 do not produce equal changes of
do not produce equal changes of 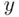 . In fact, these changes are smaller when
. In fact, these changes are smaller when 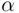 is small. Consequently, a device that chooses angles
is small. Consequently, a device that chooses angles  at random will tend to produce more intersections of the diameter that are farther from the center (i.e., more chords will be shorter).
at random will tend to produce more intersections of the diameter that are farther from the center (i.e., more chords will be shorter).










