Robert Bartoszynski - Probability and Statistical Inference

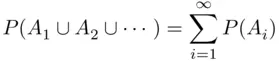
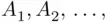for every sequence of pairwise disjoint events ( such that 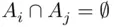for all ).

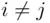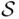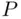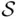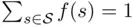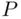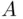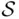If the sample space is finite or countable, one can define a probability function as follows: Let be a nonnegative function defined on , satisfying the condition . Then, may be defined for every subset of as 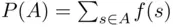. One can easily check that 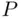satisfies all three axioms.

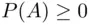Indeed, because 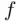is nonnegative, and 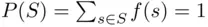. Finally, let 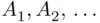be a sequence of disjoint subsets of 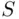. Then,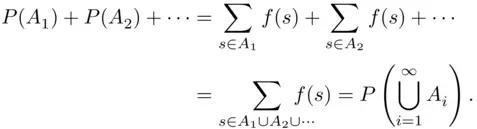

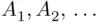Passing from the first to the second line is allowed because are disjoint, so each term appears only once. The sum in the second line is well defined (i.e., it does not depend on the order of summation because the terms are nonnegative).

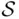However, if is not countable, one usually needs to replace summation by integration, 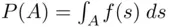. This imposes some conditions on functions 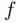and on the class of events 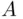. For a detailed discussion, the reader is referred to more advanced probability texts (e.g., Chung, 2001).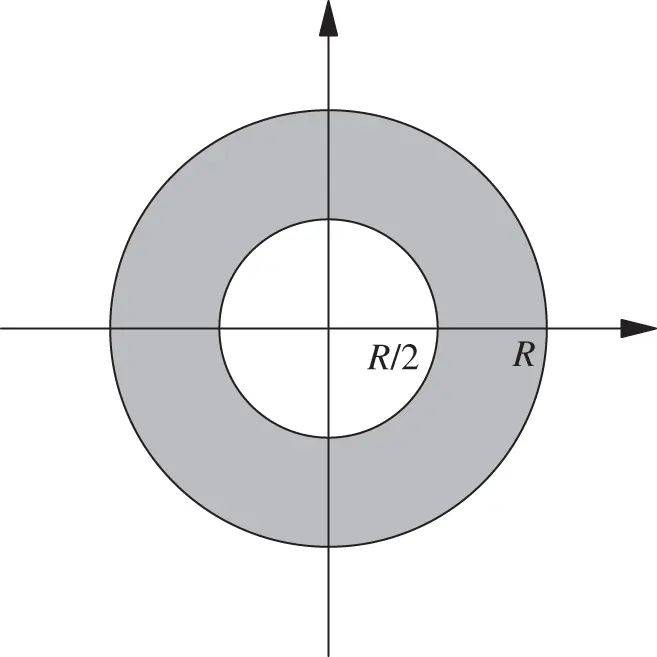

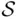Figure 2.1Hitting a target.

One of the first examples of an uncountable sample space is associated with “the random choice of a point from a set.” This phrase is usually taken to mean the following: a point is selected at random from a certain set in a finite‐dimensional space (line, plane, etc.), where 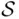has finite measure (length, area, etc.), denoted generally by 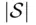. The choice is such that if 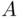( 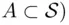has measure 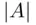, then the probability of the chosen point falling into 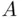is proportional to 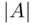. Identifying 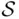with the sample space, we can then write .

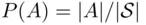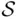To better see this, suppose that in shooting at a circular target , one is certain to score a hit, and that the point where one hits 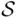is assumed to be chosen at random in the way described above. What is the probability that the point of hit is farther from the center than half of the radius of the target?