A point moves randomly on the plane, and its location is recorded at some time 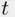 . The outcome of this experiment is the pair
. The outcome of this experiment is the pair 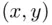 of coordinates of the observed location of the point (e.g., imagine here the location of a particle of dust in a liquid, tossed about by random hits from molecules of the medium, and performing Brownian motion; or imagine a location of a previously marked bird at the time of its capture in a bird migration study or the ages of both husband and wife at the time one of them dies).
of coordinates of the observed location of the point (e.g., imagine here the location of a particle of dust in a liquid, tossed about by random hits from molecules of the medium, and performing Brownian motion; or imagine a location of a previously marked bird at the time of its capture in a bird migration study or the ages of both husband and wife at the time one of them dies).
In any study of this kind (regardless of its ultimate purpose), the “natural” sample space 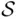 is a plane or part of the plane, (the positive quadrant, etc.). The “simple” events here are of the form
is a plane or part of the plane, (the positive quadrant, etc.). The “simple” events here are of the form 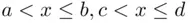 , that is, rectangles with sides parallel to the axes. The reason for distinguishing these events as “simple” is that, as will be explained in later chapters, it is often easy to assign probabilities to these events. The reason for the particular configuration of strict and nonstrict inequalities (i.e., north and east side included, south and west side excluded) will also become apparent from the analysis below. To simplify the language, we will call such events Rectangles, and use a capital letter to signify the specific assumption about which sides are included and which are not. Naturally, we will allow for infinite Rectangles, such as
, that is, rectangles with sides parallel to the axes. The reason for distinguishing these events as “simple” is that, as will be explained in later chapters, it is often easy to assign probabilities to these events. The reason for the particular configuration of strict and nonstrict inequalities (i.e., north and east side included, south and west side excluded) will also become apparent from the analysis below. To simplify the language, we will call such events Rectangles, and use a capital letter to signify the specific assumption about which sides are included and which are not. Naturally, we will allow for infinite Rectangles, such as 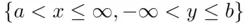 .
.
It is easy to determine the field generated by all Rectangles: These are events that result from finite operations on Rectangles. Clearly, the complement of a Rectangle is a union of at most eight disjoint (infinite) Rectangles (see Figure 1.7), whereas the intersection of Rectangles is again a Rectangle (or is empty). Since unions are reduced to intersections of complements by De Morgan's laws, every element of the smallest field containing all Rectangles is the union of a finite number of disjoint Rectangles. On the other hand, there exist events that do not belong to this field of events. As a simple example, one might be interested in the event that the point 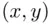 lies within distance
lies within distance 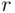 from some fixed point (from the initial location of the particle, the point of release of the bird, etc.). This event is a circle on the plane, and hence a subset of
from some fixed point (from the initial location of the particle, the point of release of the bird, etc.). This event is a circle on the plane, and hence a subset of  which is not decomposable into a finite number of Rectangles. On the other hand, a circle does belong to the
which is not decomposable into a finite number of Rectangles. On the other hand, a circle does belong to the 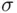 ‐field spanned by Rectangles: it is representable as a countable union of Rectangles, or equivalently, as an infinite intersection of sets built up of Rectangles.
‐field spanned by Rectangles: it is representable as a countable union of Rectangles, or equivalently, as an infinite intersection of sets built up of Rectangles.
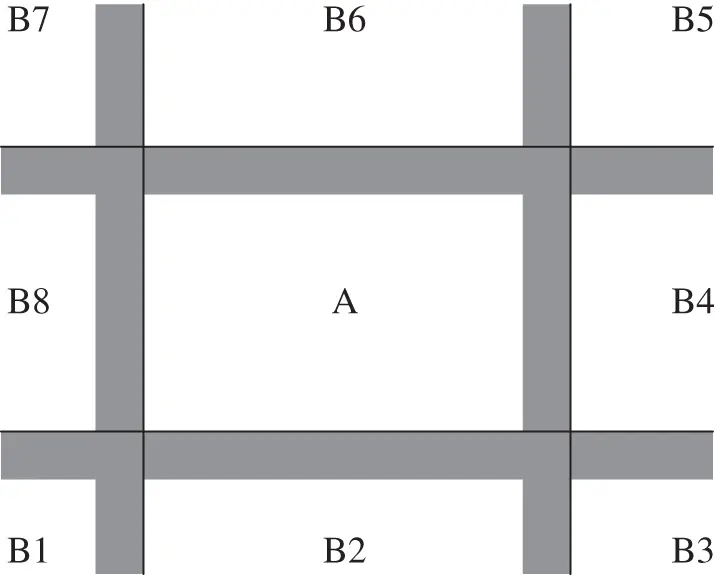
Figure 1.7Complement of a Rectangle.
Similarly, in this example there are other events, which are not in the field generated by Rectangles and which could be considered, such as triangles, rectangles with sides not parallel to the axes, and ellipses.
Take an experiment consisting of tossing a coin infinitely many times. The “natural” sample space 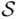 is the space of all infinite sequences
is the space of all infinite sequences 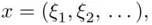 where
where 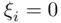 or 1 (or any other two distinct symbols representing heads and tails). The “simple” events here are of the form “heads on the
or 1 (or any other two distinct symbols representing heads and tails). The “simple” events here are of the form “heads on the 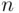 th toss,” that is, sets of all infinite sequences
th toss,” that is, sets of all infinite sequences 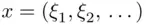 with the
with the 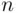 th coordinate
th coordinate 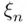 satisfying
satisfying 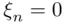 . The events in the field generated by the simple events are of the form “heads on tosses
. The events in the field generated by the simple events are of the form “heads on tosses  and tails on tosses
and tails on tosses  ,” with both
,” with both  and
and 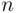 finite and the outcomes of all other tosses remaining unspecified.
finite and the outcomes of all other tosses remaining unspecified.
An event that does not belong to this field, but does belong to the 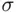 ‐field generated by the simple events, is the event that “as the number of tosses increases, the frequency of heads approaches a limit.” Clearly, to determine whether or not this event occurs, it does not suffice to know any finite number of coordinates
‐field generated by the simple events, is the event that “as the number of tosses increases, the frequency of heads approaches a limit.” Clearly, to determine whether or not this event occurs, it does not suffice to know any finite number of coordinates 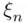 .
.
To generalize this example, replace the outcome of the coin tosses by the result of some experiment repeated infinitely many times. This way the coordinate 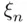 carries more information than it does for the outcome of
carries more information than it does for the outcome of  th coin toss. The “simple” events are now of the form of sets of sequences
th coin toss. The “simple” events are now of the form of sets of sequences 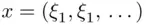 with
with 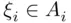 for
for 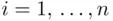 , while the
, while the 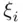 's for
's for 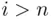 are unconstrained. Here
are unconstrained. Here  are events that occur at the first
are events that occur at the first 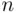 times of observations. The “simple” events described above, of an obvious interest and importance both in applications and in building the theory, are called “cylinder” events. The smallest
times of observations. The “simple” events described above, of an obvious interest and importance both in applications and in building the theory, are called “cylinder” events. The smallest 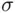 ‐field containing all cylinder events comprises all events that may be of interest, including those that are obtained through limits of sequences of cylinder events.
‐field containing all cylinder events comprises all events that may be of interest, including those that are obtained through limits of sequences of cylinder events.
Читать дальше

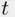 . The outcome of this experiment is the pair
. The outcome of this experiment is the pair 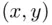 of coordinates of the observed location of the point (e.g., imagine here the location of a particle of dust in a liquid, tossed about by random hits from molecules of the medium, and performing Brownian motion; or imagine a location of a previously marked bird at the time of its capture in a bird migration study or the ages of both husband and wife at the time one of them dies).
of coordinates of the observed location of the point (e.g., imagine here the location of a particle of dust in a liquid, tossed about by random hits from molecules of the medium, and performing Brownian motion; or imagine a location of a previously marked bird at the time of its capture in a bird migration study or the ages of both husband and wife at the time one of them dies).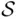 is a plane or part of the plane, (the positive quadrant, etc.). The “simple” events here are of the form
is a plane or part of the plane, (the positive quadrant, etc.). The “simple” events here are of the form 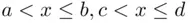 , that is, rectangles with sides parallel to the axes. The reason for distinguishing these events as “simple” is that, as will be explained in later chapters, it is often easy to assign probabilities to these events. The reason for the particular configuration of strict and nonstrict inequalities (i.e., north and east side included, south and west side excluded) will also become apparent from the analysis below. To simplify the language, we will call such events Rectangles, and use a capital letter to signify the specific assumption about which sides are included and which are not. Naturally, we will allow for infinite Rectangles, such as
, that is, rectangles with sides parallel to the axes. The reason for distinguishing these events as “simple” is that, as will be explained in later chapters, it is often easy to assign probabilities to these events. The reason for the particular configuration of strict and nonstrict inequalities (i.e., north and east side included, south and west side excluded) will also become apparent from the analysis below. To simplify the language, we will call such events Rectangles, and use a capital letter to signify the specific assumption about which sides are included and which are not. Naturally, we will allow for infinite Rectangles, such as 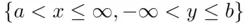 .
.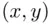 lies within distance
lies within distance 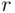 from some fixed point (from the initial location of the particle, the point of release of the bird, etc.). This event is a circle on the plane, and hence a subset of
from some fixed point (from the initial location of the particle, the point of release of the bird, etc.). This event is a circle on the plane, and hence a subset of  which is not decomposable into a finite number of Rectangles. On the other hand, a circle does belong to the
which is not decomposable into a finite number of Rectangles. On the other hand, a circle does belong to the 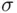 ‐field spanned by Rectangles: it is representable as a countable union of Rectangles, or equivalently, as an infinite intersection of sets built up of Rectangles.
‐field spanned by Rectangles: it is representable as a countable union of Rectangles, or equivalently, as an infinite intersection of sets built up of Rectangles.
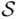 is the space of all infinite sequences
is the space of all infinite sequences 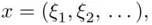 where
where 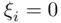 or 1 (or any other two distinct symbols representing heads and tails). The “simple” events here are of the form “heads on the
or 1 (or any other two distinct symbols representing heads and tails). The “simple” events here are of the form “heads on the 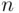 th toss,” that is, sets of all infinite sequences
th toss,” that is, sets of all infinite sequences 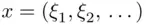 with the
with the 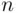 th coordinate
th coordinate 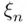 satisfying
satisfying 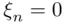 . The events in the field generated by the simple events are of the form “heads on tosses
. The events in the field generated by the simple events are of the form “heads on tosses  and tails on tosses
and tails on tosses  ,” with both
,” with both  and
and 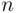 finite and the outcomes of all other tosses remaining unspecified.
finite and the outcomes of all other tosses remaining unspecified.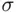 ‐field generated by the simple events, is the event that “as the number of tosses increases, the frequency of heads approaches a limit.” Clearly, to determine whether or not this event occurs, it does not suffice to know any finite number of coordinates
‐field generated by the simple events, is the event that “as the number of tosses increases, the frequency of heads approaches a limit.” Clearly, to determine whether or not this event occurs, it does not suffice to know any finite number of coordinates 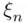 .
.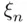 carries more information than it does for the outcome of
carries more information than it does for the outcome of  th coin toss. The “simple” events are now of the form of sets of sequences
th coin toss. The “simple” events are now of the form of sets of sequences 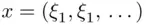 with
with 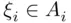 for
for 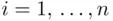 , while the
, while the 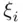 's for
's for 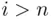 are unconstrained. Here
are unconstrained. Here  are events that occur at the first
are events that occur at the first 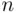 times of observations. The “simple” events described above, of an obvious interest and importance both in applications and in building the theory, are called “cylinder” events. The smallest
times of observations. The “simple” events described above, of an obvious interest and importance both in applications and in building the theory, are called “cylinder” events. The smallest 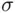 ‐field containing all cylinder events comprises all events that may be of interest, including those that are obtained through limits of sequences of cylinder events.
‐field containing all cylinder events comprises all events that may be of interest, including those that are obtained through limits of sequences of cylinder events.










