Robert Bartoszynski - Probability and Statistical Inference
Здесь есть возможность читать онлайн «Robert Bartoszynski - Probability and Statistical Inference» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Probability and Statistical Inference
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Probability and Statistical Inference: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Probability and Statistical Inference»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Probability and Statistical Inference, Third Edition
Probability and Statistical Inference

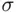 ‐fields. This is illustrated by the following example:
‐fields. This is illustrated by the following example: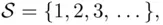 and let
and let 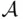 be the class of all subsets
be the class of all subsets 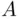 of
of 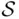 such that either
such that either 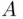 or
or 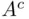 is finite. Then
is finite. Then 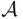 is a field but not a
is a field but not a 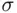 ‐field. First, if
‐field. First, if 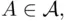 then
then 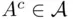 because the definition of
because the definition of 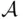 is symmetric with respect to complementation. Next, if
is symmetric with respect to complementation. Next, if 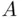 and
and 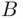 are both in
are both in 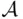 , so is their union. If
, so is their union. If 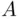 and
and 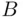 are both finite, then
are both finite, then  is finite and hence belongs to
is finite and hence belongs to 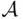 . On the other hand, if either
. On the other hand, if either 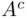 or
or 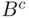 (or both) are finite, then
(or both) are finite, then 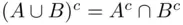 is also finite because it is contained in
is also finite because it is contained in 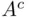 and also in
and also in 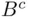 .
.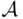 is a field. However,
is a field. However, 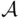 is not a
is not a 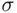 ‐field. Let
‐field. Let 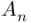 be the set consisting only of the element
be the set consisting only of the element 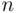 (i.e.,
(i.e., 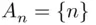 ). Clearly,
). Clearly, 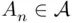 . Take now
. Take now 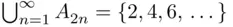 . This is a countable union of sets in
. This is a countable union of sets in 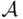 that is not in
that is not in 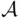 since the set of all even numbers is not finite, nor does it have a finite complement.
since the set of all even numbers is not finite, nor does it have a finite complement.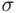 ‐field can be difficult. On the other hand, it is sometimes easy to verify that a class of sets is a monotone class.
‐field can be difficult. On the other hand, it is sometimes easy to verify that a class of sets is a monotone class.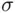 ‐field is a monotone class. Conversely, a field that is a monotone class is a
‐field is a monotone class. Conversely, a field that is a monotone class is a 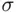 ‐field.
‐field.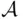 is a
is a 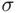 ‐field, and let
‐field, and let 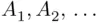 be a monotone sequence of elements of
be a monotone sequence of elements of 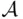 . If
. If 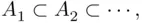 then
then 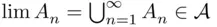 , whereas if
, whereas if 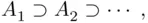 then
then 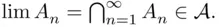 So
So 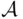 is a monotone class. On the other hand, let
is a monotone class. On the other hand, let 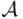 be a monotone class and a field, and let
be a monotone class and a field, and let 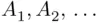 be an arbitrary sequence of elements of
be an arbitrary sequence of elements of  . Put
. Put 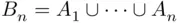 . Then since
. Then since 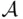 is a field, and also
is a field, and also 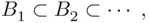
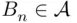 for every
for every 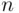 . Further, since
. Further, since 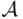 is a monotone class,
is a monotone class, 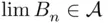 . However,
. However, 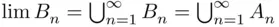 , so
, so 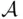 is a
is a  ‐field, as asserted.
‐field, as asserted.










