1 1.3.1 Answer true or false. Justify your answer. (i) If and are distinct events (i.e., ) such that and are disjoint, then and are also disjoint. (ii) If and are disjoint, then and are also disjoint. (iii) If and are disjoint, and also and are disjoint, then and are disjoint. (iv) If and are both contained in , then . (v) If is contained in , is contained in and is disjoint from , then is disjoint from . (vi) If , then .
2 1.3.2 In the statements below , and are events. Find those statements or formulas that are true. (i) If , then . (ii) . (iii) . (iv) If , then . (v) . (vi) . (vii) . (viii) If , and , then . (ix) If , and are not empty, then is not empty. (x) Show that .
3 1.3.3 Find if: (i) . (ii) . (iii) . (iv) .
4 1.3.4 In a group of 1,000 students of a certain college, 60 take French, 417 take calculus, and 509 take statistics. Moreover, 20 take French and calculus, 17 take French and statistics, and 147 take statistics and calculus. However, 196 students do not take any of these three subjects. Determine the number of students who take French, calculus, and statistics.
5 1.3.5 Let , and be three events. Match, where possible, events through with events through . Matching means that the events are exactly the same; that is, if one occurs, so must the other and conversely (see the Definition 1.3.2). (Hint: Draw a Venn diagram for each event do the same for events , and then compare the diagrams.)Among events , , : two or more occur. exactly one occurs. only occurs. all occur. none occurs. at most one occurs. at least one occurs. exactly two occur. no more than two occur. occurs.
6 1.3.6 A standard deck of cards is dealt among players and . Let be the event “ has at least aces,” and let , and be defined similarly. For each of the events below, determine the number of aces that has. (i) . (ii) . (iii) . (iv) . (v) . (vi) .
7 1.3.7 Five burglars, and , divide the loot, consisting of five identical gold bars and four identical diamonds. Let be the event that got at least gold bars and at most diamonds. Let denote analogous events for burglars (e.g., is the event that got 2, 3, 4, or 5 gold bars and 0 or 1 diamond). Determine the number of gold bars and the number of diamonds received by if the following events occur (if determination of and/or is impossible, give the range of values): (i) . (ii) . (iii) . (iv) .
8 1.3.8 Let be defined inductively by . Find and for .
1.4 Infinite Operations on Events
As already mentioned, the operations of union and intersection can be extended to infinitely many events. Let 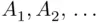 be an infinite sequence of events. Then,
be an infinite sequence of events. Then,
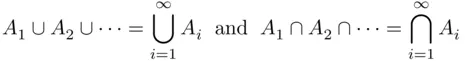
are events “at least one 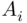 occurs” and “all
occurs” and “all 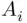 's occur,” respectively.
's occur,” respectively.
If at least one event 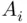 occurs, then there is one that occurs first. This remark leads to the following useful decomposition of a union of events into a union of disjoint events:
occurs, then there is one that occurs first. This remark leads to the following useful decomposition of a union of events into a union of disjoint events:
(1.6) 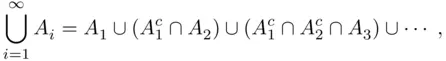
where 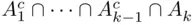 is the event “
is the event “ 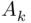 is the first event in the sequence that occurs.”
is the first event in the sequence that occurs.”
For an infinite sequence 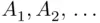 one can define two events:
one can define two events:
(1.7) 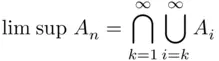
and
(1.8) 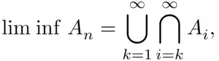
these being, respectively, the event that “infinitely many 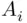 's occur” and the event that “all except finitely many
's occur” and the event that “all except finitely many 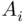 's occur.” Here the inner union in the event ( 1.7) is the event “at least one event
's occur.” Here the inner union in the event ( 1.7) is the event “at least one event 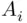 with
with 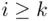 will occur”; call this event
will occur”; call this event 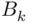 . The intersection over
. The intersection over 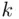 means that the event
means that the event 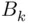 occurs for every
occurs for every 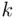 . No matter how large
. No matter how large 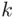 we take, there will be at least one event
we take, there will be at least one event 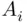 with
with 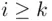 that will occur. But this is possible only if infinitely many
that will occur. But this is possible only if infinitely many 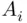 s occur.
s occur.
For the event 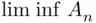 , the argument is similar. The intersection
, the argument is similar. The intersection 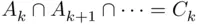 occurs if all events
occurs if all events 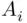 with
with 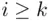 occur. The union
occur. The union 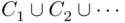 means that at least one of the events
means that at least one of the events 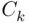 will occur, and that means that all
will occur, and that means that all 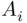 will occur, except possibly finitely many.
will occur, except possibly finitely many.
Читать дальше

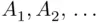 be an infinite sequence of events. Then,
be an infinite sequence of events. Then,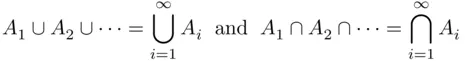
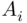 occurs” and “all
occurs” and “all 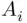 's occur,” respectively.
's occur,” respectively.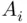 occurs, then there is one that occurs first. This remark leads to the following useful decomposition of a union of events into a union of disjoint events:
occurs, then there is one that occurs first. This remark leads to the following useful decomposition of a union of events into a union of disjoint events: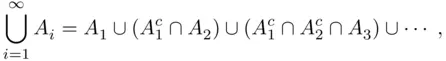
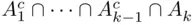 is the event “
is the event “ 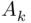 is the first event in the sequence that occurs.”
is the first event in the sequence that occurs.”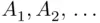 one can define two events:
one can define two events: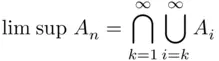
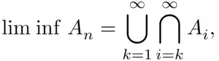
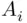 's occur” and the event that “all except finitely many
's occur” and the event that “all except finitely many 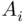 's occur.” Here the inner union in the event ( 1.7) is the event “at least one event
's occur.” Here the inner union in the event ( 1.7) is the event “at least one event 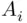 with
with 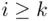 will occur”; call this event
will occur”; call this event 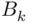 . The intersection over
. The intersection over 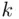 means that the event
means that the event 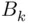 occurs for every
occurs for every 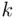 . No matter how large
. No matter how large 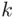 we take, there will be at least one event
we take, there will be at least one event 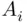 with
with 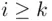 that will occur. But this is possible only if infinitely many
that will occur. But this is possible only if infinitely many 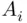 s occur.
s occur.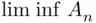 , the argument is similar. The intersection
, the argument is similar. The intersection 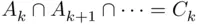 occurs if all events
occurs if all events 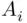 with
with 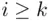 occur. The union
occur. The union 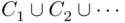 means that at least one of the events
means that at least one of the events 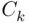 will occur, and that means that all
will occur, and that means that all 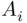 will occur, except possibly finitely many.
will occur, except possibly finitely many.










