Robert Bartoszynski - Probability and Statistical Inference
Здесь есть возможность читать онлайн «Robert Bartoszynski - Probability and Statistical Inference» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Probability and Statistical Inference
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Probability and Statistical Inference: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Probability and Statistical Inference»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Probability and Statistical Inference, Third Edition
Probability and Statistical Inference

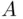 implies (or entails )
implies (or entails ) 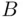 .
.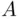 and
and 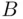 are said to be equal ,
are said to be equal , 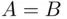 , if
, if 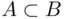 and
and 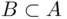 .
.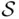 consisting of four outcomes: HH, HT, TH, and TT. The event
consisting of four outcomes: HH, HT, TH, and TT. The event 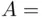 “heads in the first toss”
“heads in the first toss” 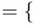 HH, HT} is contained in the event
HH, HT} is contained in the event 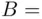 “at least one head”
“at least one head” 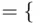 HH, HT, TH}. The events “the results alternate” and “at least one head and one tail” imply one another, and hence are equal.
HH, HT, TH}. The events “the results alternate” and “at least one head and one tail” imply one another, and hence are equal.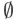 . The event corresponding to
. The event corresponding to 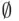 is called a null ( impossible ) event.
is called a null ( impossible ) event.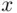 such that
such that 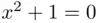 are both empty, but one consists of people and the other of numbers, so they cannot be equal. This is not so, however, as is shown by the following formal argument (to appreciate this argument, one needs some training in logic). Suppose that
are both empty, but one consists of people and the other of numbers, so they cannot be equal. This is not so, however, as is shown by the following formal argument (to appreciate this argument, one needs some training in logic). Suppose that 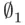 and
and 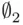 are two empty sets. To prove that they are equal, one needs to prove that
are two empty sets. To prove that they are equal, one needs to prove that 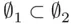 and
and 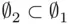 . Formally, the first inclusion is the implication: “if
. Formally, the first inclusion is the implication: “if 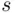 belongs to
belongs to 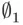 , then
, then 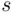 belongs to
belongs to 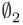 .” This implication is true, because its premise is false: there is no
.” This implication is true, because its premise is false: there is no 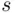 that belongs to
that belongs to 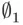 . The same holds for the second implication, so
. The same holds for the second implication, so 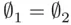 .
.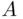 will be called the complement of
will be called the complement of 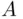 and denoted
and denoted 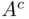 , to be read also as “not
, to be read also as “not 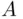 .”
.”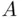 or to
or to 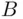 (so possibly to both of them) is called the union of
(so possibly to both of them) is called the union of 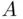 and
and 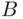 and denoted
and denoted  , to be read as “
, to be read as “ 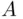 or
or 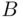 .”
.”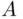 and
and 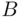 is called the intersection of
is called the intersection of 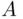 and
and 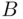 and denoted
and denoted  .
.










