The following examples show experiments and corresponding sample spaces with sample points that are only partially observable :
Candidates for a certain job are characterized by their level 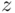 of skills required for the job. The actual value of
of skills required for the job. The actual value of 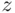 is not observable, though; what we observe is the candidate's score
is not observable, though; what we observe is the candidate's score 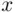 on a certain test. Thus, the sample point in
on a certain test. Thus, the sample point in 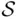 is a pair
is a pair 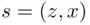 , and only one coordinate of
, and only one coordinate of 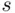 ,
,  , is observable.
, is observable.
The objective might be to find selection thresholds 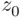 and
and 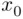 , such that the rule: “accept all candidates whose score
, such that the rule: “accept all candidates whose score  exceeds
exceeds 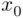 ” would lead to maximizing the (unobservable) number of persons accepted whose true level of skill
” would lead to maximizing the (unobservable) number of persons accepted whose true level of skill 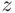 exceeds
exceeds 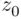 . Naturally, to find such a solution, one needs to understand statistical relation between observable
. Naturally, to find such a solution, one needs to understand statistical relation between observable 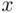 and unobservable
and unobservable 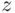 .
.
Another example when the points in the sample space are only partially observable concerns studies of incidence of activities about which one may hesitate to respond truthfully, or even to respond at all. These are typically studies related to sexual habits or preferences, abortion, law and tax violation, drug use, and so on.
Example 1.9 Randomized Response
Let 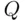 be the activity analyzed, and assume that the researcher is interested in the frequency of persons who ever participated in activity
be the activity analyzed, and assume that the researcher is interested in the frequency of persons who ever participated in activity 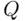 (for simplicity, we will call them
(for simplicity, we will call them 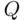 ‐persons). It ought to be stressed that the objective is not to identify the
‐persons). It ought to be stressed that the objective is not to identify the 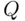 ‐persons, but only to find the proportion of such persons in the population.
‐persons, but only to find the proportion of such persons in the population.
The direct question reduced to something like “Are you a 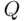 ‐person?” is not likely to be answered truthfully, if at all. It is therefore necessary to make the respondent safe, guaranteeing that their responses will reveal nothing about them as regards
‐person?” is not likely to be answered truthfully, if at all. It is therefore necessary to make the respondent safe, guaranteeing that their responses will reveal nothing about them as regards 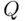 . This can be accomplished as follows: The respondent is given a pair of distinguishable dice, for example, one green and one white. She throws them both at the same time, in such a way that the experimenter does not know the results of the toss (e.g., the dice are in a box and only the respondent looks into the box after it is shaken). The instruction is the following: If the green die shows an odd face (1, 3, or 5), then respond to the question “Are you a
. This can be accomplished as follows: The respondent is given a pair of distinguishable dice, for example, one green and one white. She throws them both at the same time, in such a way that the experimenter does not know the results of the toss (e.g., the dice are in a box and only the respondent looks into the box after it is shaken). The instruction is the following: If the green die shows an odd face (1, 3, or 5), then respond to the question “Are you a 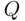 ‐person?” If the green die shows an even face (2, 4, or 6), then respond to the question, “Does the white die show an ace?” The scheme of this response is summarized by the flowchart in Figure 1.4.
‐person?” If the green die shows an even face (2, 4, or 6), then respond to the question, “Does the white die show an ace?” The scheme of this response is summarized by the flowchart in Figure 1.4.
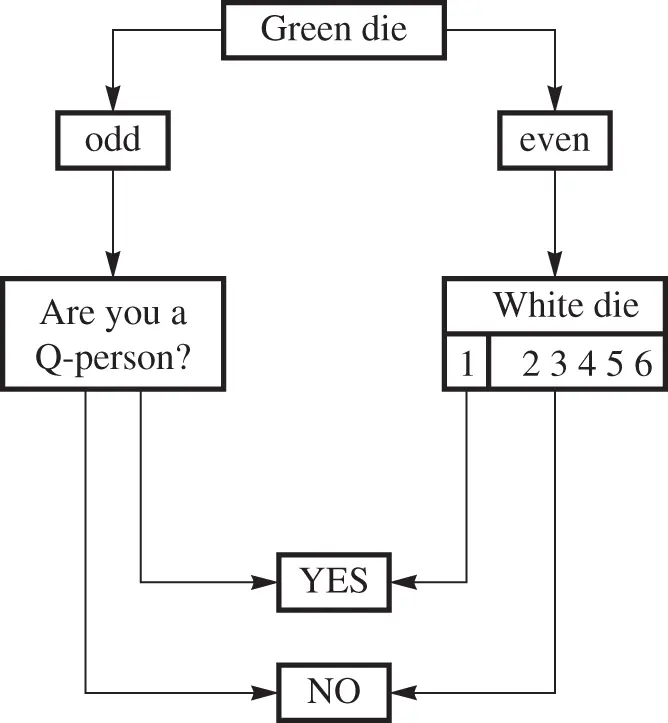
Figure 1.4Scheme of a randomized response.
The interviewer knows the answer “yes” or “no” but does not know whether it is the answer to the question about 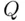 or the question about the white die. Here a natural sample space consists of points
or the question about the white die. Here a natural sample space consists of points 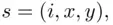 where
where 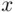 and
and 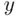 are outcomes on green and white die, respectively, while
are outcomes on green and white die, respectively, while 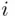 is 1 or 0 depending on whether or not the respondent is a
is 1 or 0 depending on whether or not the respondent is a 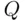 ‐person. We have
‐person. We have 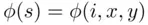 = “yes” if
= “yes” if 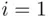 and
and 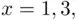 or 5 for any
or 5 for any 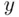 , or if
, or if 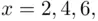 and
and  for any
for any 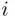 . In all other cases,
. In all other cases, 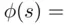 “no.”
“no.”
Читать дальше

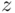 of skills required for the job. The actual value of
of skills required for the job. The actual value of 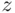 is not observable, though; what we observe is the candidate's score
is not observable, though; what we observe is the candidate's score 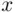 on a certain test. Thus, the sample point in
on a certain test. Thus, the sample point in 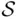 is a pair
is a pair 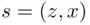 , and only one coordinate of
, and only one coordinate of 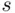 ,
,  , is observable.
, is observable.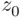 and
and 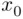 , such that the rule: “accept all candidates whose score
, such that the rule: “accept all candidates whose score  exceeds
exceeds 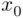 ” would lead to maximizing the (unobservable) number of persons accepted whose true level of skill
” would lead to maximizing the (unobservable) number of persons accepted whose true level of skill 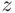 exceeds
exceeds 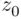 . Naturally, to find such a solution, one needs to understand statistical relation between observable
. Naturally, to find such a solution, one needs to understand statistical relation between observable 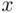 and unobservable
and unobservable 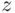 .
.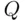 be the activity analyzed, and assume that the researcher is interested in the frequency of persons who ever participated in activity
be the activity analyzed, and assume that the researcher is interested in the frequency of persons who ever participated in activity 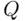 (for simplicity, we will call them
(for simplicity, we will call them 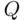 ‐persons). It ought to be stressed that the objective is not to identify the
‐persons). It ought to be stressed that the objective is not to identify the 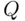 ‐persons, but only to find the proportion of such persons in the population.
‐persons, but only to find the proportion of such persons in the population.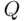 ‐person?” is not likely to be answered truthfully, if at all. It is therefore necessary to make the respondent safe, guaranteeing that their responses will reveal nothing about them as regards
‐person?” is not likely to be answered truthfully, if at all. It is therefore necessary to make the respondent safe, guaranteeing that their responses will reveal nothing about them as regards 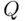 . This can be accomplished as follows: The respondent is given a pair of distinguishable dice, for example, one green and one white. She throws them both at the same time, in such a way that the experimenter does not know the results of the toss (e.g., the dice are in a box and only the respondent looks into the box after it is shaken). The instruction is the following: If the green die shows an odd face (1, 3, or 5), then respond to the question “Are you a
. This can be accomplished as follows: The respondent is given a pair of distinguishable dice, for example, one green and one white. She throws them both at the same time, in such a way that the experimenter does not know the results of the toss (e.g., the dice are in a box and only the respondent looks into the box after it is shaken). The instruction is the following: If the green die shows an odd face (1, 3, or 5), then respond to the question “Are you a 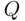 ‐person?” If the green die shows an even face (2, 4, or 6), then respond to the question, “Does the white die show an ace?” The scheme of this response is summarized by the flowchart in Figure 1.4.
‐person?” If the green die shows an even face (2, 4, or 6), then respond to the question, “Does the white die show an ace?” The scheme of this response is summarized by the flowchart in Figure 1.4.
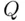 or the question about the white die. Here a natural sample space consists of points
or the question about the white die. Here a natural sample space consists of points 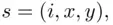 where
where 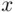 and
and 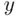 are outcomes on green and white die, respectively, while
are outcomes on green and white die, respectively, while 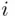 is 1 or 0 depending on whether or not the respondent is a
is 1 or 0 depending on whether or not the respondent is a 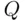 ‐person. We have
‐person. We have 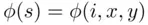 = “yes” if
= “yes” if 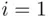 and
and 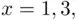 or 5 for any
or 5 for any 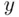 , or if
, or if 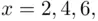 and
and  for any
for any 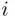 . In all other cases,
. In all other cases, 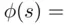 “no.”
“no.”










