Robert Bartoszynski - Probability and Statistical Inference

One could wonder what is a possible advantage, if any, of not knowing the question asked and observing only the answer. This does not make sense if we need to know the truth about each individual respondent. However, one should remember that we are only after the overall frequency of 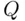‐persons.

We are in fact “contaminating” the question by making the respondent answer either a 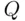‐question or some other auxiliary question. But this is a “controlled contamination”: we know how often (on average) the respondents answer the auxiliary question, and how often their answer is “yes.” Consequently, as we will see in Chapter 11, we can still make an inference about the proportion of 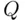‐persons based on the observed responses.

1 1.2.1 List all sample points in sample spaces for the following experiments: (i) We toss a balanced coin. 1 If heads come up, we toss a die. Otherwise, we toss the coin two more times. (ii) A coin is tossed until the total of two tails occurs, but no more than four times (i.e., a coin is tossed until the second tail or fourth toss, whichever comes first).

2 1.2.2 Alice, Bob, Carl, and Diana enter the elevator on the first floor of a four‐story building. Each of them leaves the elevator on either the second, third, or fourth floor. (i) Describe the sample space without listing all sample points. (ii) List all sample points such that Carl and Diana leave the elevator on the third floor. (iii) List all sample points if Carl and Diana leave the elevator at the same floor.

3 1.2.3 An urn contains five chips, labeled . Three chips are selected. List all outcomes included in the event “the second largest number drawn was 3.”

4 1.2.4 In a game of craps, the player rolls a pair of dice. If he gets a total of 7 or 11, he wins at once; if the total is 2, 3, or 12, he loses at once. Otherwise, the sum, say , is his “point,” and he keeps rolling dice until either he rolls another (in which case he wins) or he rolls a 7 in which case he loses. Describe the event “the player wins with a point of 5.”

5 1.2.5 The experiment consists of placing six balls in three boxes. List all outcomes in the sample space if: (i) The balls are indistinguishable, but the boxes are distinguishable. (Hint: There are 28 different placements.) (ii) Neither the balls nor the boxes are distinguishable. (iii) Two balls are white and four are red; the boxes are distinguishable.

6 1.2.6 John and Mary plan to meet each other. Each of them is to arrive at the meeting place at some time between 5 p.m. and 6 p.m. John is to wait 20 minutes (or until 6 p.m., whichever comes first), and then leave if Mary does not show up. Mary will wait only 5 minutes (or until 6 p.m., whichever comes first), and then leave if John does not show up. Letting and denote the arrival times of John and Mary, determine the sample space and describe events (i)–(viii) by drawing pictures, or by appropriate inequalities for and . If you think that the description is impossible, say so. (i) John arrives before Mary does. (ii) John and Mary meet. (iii) Either Mary comes first, or they do not meet. (iv) Mary comes first, but they do not meet. (v) John comes very late. (vi) They arrive less than 15 minutes apart, and they do not meet. (vii) Mary arrives at 5:15 p.m. and meets John, who is already there. (viii) They almost miss one another.Problems 1.2.7–1.2.8 show an importance of the sample space selection.

7 1.2.7 Let be the experiment consisting of tossing a coin three times, with H and T standing for heads and tails, respectively.The following set of outcomes is an incomplete list of the points of the sample space of the experiment : {HHH, HTT, TTT, HHT, HTH, THH}. Use a tree diagram to find the missing outcomes.An alternative sample space for the same experiment consists of the following four outcomes: no heads , one head , two heads and three heads . Which of the following events can be described as subsets of but not as subsets of ? More than two heads. Head on the second toss. More tails than heads. At least one tail, with head on the last toss. At least two faces the same. Head and tail alternate.Still another sample space for the experiment consists of the four outcomes and . The first coordinate is 1 if the first two tosses show the same face and 0 otherwise; the second coordinate is 1 if the last two tosses show the same face, and 0 otherwise. For instance, if we observe HHT, the outcome is . List the outcomes of that belong to the event of .Which of the following events can be represented as subsets of , but cannot be represented as subsets of ? First and third toss show the same face. Heads on all tosses. All faces the same. Each face appears at least once. More heads than tails.

8 1.2.8 Let be an experiment consisting of tossing a die twice. Let be the sample space with sample points with and being the numbers of dots that appear in the first and second toss, respectively.(i) Let be the sample space for the experiment consisting of all possible sums so that . Which of the following events can be defined as subsets of but not of ? One face odd, the other even. Both faces even. Faces different. Result on the first toss less than the result on the second. Product greater than 10. Product greater than 30.(ii) Let be the sample space for the experiment consisting of all possible absolute values of the difference so that . Which of the following events can be defined as subsets of but not of ? One face shows twice as many dots as the other, Faces the same, One face shows six times as many dots as the other, One face odd, the other even, The ratio of the numbers of dots on the faces is different from 1.

9 1.2.9 Referring to Example 1.9, suppose that we modify it as follows: The respondent tosses a green die (with the outcome unknown to the interviewer). If the outcome is odd, he responds to the Q‐question; otherwise, he responds to the question “Were you born in April?” Again, the interviewer observes only the answer “yes” or “no.” Apart from the obvious difference in the frequency of the answer “yes” to the auxiliary question (on the average 1 in 12 instead of 1 in 6), are there any essential differences between this scheme and the scheme in Example 1.9? Explain your answer.

Next, we introduce concepts that will allow us to form composite events out of simpler ones. We begin with the relations of inclusion and equality .

Definition 1.3.1The event 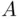is contained in the event 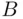, or 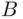contains 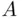, if every sample point of 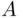is also a sample point of 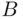. Whenever this is true, we will write 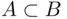, or equivalently, .