Judging from the failures of weather forecasts, to more spectacular prediction failures, such as bankruptcies of large companies and stock market crashes, it would appear that statistical methods do not perform very well. However, with a possible exception of weather forecasting, these examples are, at best, only partially statistical predictions. Moreover, failures tend to be better remembered than successes. Whatever the case, statistical methods are at present, and are likely to remain indefinitely, our best and most reliable prediction tools.
To make decisions under uncertainty, one usually needs to collect some data . Data may come from past experiences and observations, or may result from some controlled processes, such as laboratory or field experiments. The data are then used to hypothesize about the laws (often called mechanisms ) that govern the fragment of reality of interest. In our book, we are interested in laws expressed in probabilistic terms: They specify directly, or allow us to compute, the chances of some events to occur. Knowledge of these chances is, in most cases, the best one can get with regard to prediction and decisions.
Probability theory is a domain of pure mathematics and as such, it has its own conceptual structure. To enable a variety of applications (typically comprising of all areas of human endeavor, ranging from biological, medical, social and physical sciences, to engineering, humanities, business, etc.), such structure must be kept on an abstract level. An application of probability to the particular situation analyzed requires a number of initial steps in which the elements of the real situation are interpreted as abstract concepts of probability theory. Such interpretation is often referred to as building a probabilistic model of the situation at hand. How well this is done is crucial to the success of application.
One of the main concepts here is that of an experiment —a term used in a broad sense. It means any process that generates data which is influenced, at least in part, by chance.
In analyzing an experiment, one is primarily interested in its outcome —the concept that is not defined (i.e., a primitive concept ) but has to be specified in every particular application. This specification may be done in different ways, with the only requirements being that (1) outcomes exclude one another and (2) they exhaust the set of all logical possibilities.
Consider an experiment consisting of two tosses of a regular die. An outcome is most naturally represented by a pair of numbers that turn up on the upper faces of the die so that they form a pair 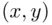 , with
, with 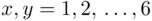 (see Table 1.1).
(see Table 1.1).
Table 1.1Outcomes on a pair of dice.
|
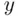 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
(1, 1) |
(1, 2) |
(1, 3) |
(1, 4) |
(1, 5) |
(1, 6) |
|
2 |
(2, 1) |
(2, 2) |
(2, 3) |
(2, 4) |
(2, 5) |
(2, 6) |
 |
3 |
(3, 1) |
(3, 2) |
(3, 3) |
(3, 4) |
(3, 5) |
(3, 6) |
|
4 |
(4, 1) |
(4, 2) |
(4, 3) |
(4, 4) |
(4, 5) |
(4, 6) |
|
5 |
(5, 1) |
(5, 2) |
(5, 3) |
(5, 4) |
(5, 5) |
(5, 6) |
|
6 |
(6, 1) |
(6, 2) |
(6, 3) |
(6, 4) |
(6, 5) |
(6, 6) |
In the case of an experiment of tossing a die three times, the outcomes will be triplets 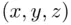 , with
, with 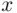 ,
, 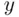 , and
, and 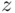 being integers between 1 and 6.
being integers between 1 and 6.
Since the outcome of an experiment is not known in advance, it is important to determine the set of all possible outcomes. This set, called the sample space , forms the conceptual framework for all further considerations of probability.
Definition 1.2.1The sample space , denoted by 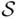 , is the set of all outcomes of an experiment. The elements of the sample space are called elementary outcomes, or sample points .
, is the set of all outcomes of an experiment. The elements of the sample space are called elementary outcomes, or sample points .
In Example 1.1, the sample space 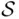 has
has 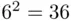 sample points in the case of two tosses, and
sample points in the case of two tosses, and 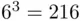 points in the case of three tosses of a die. The first statement can be verified by a direct counting of the elements of the sample space. Similar verification of the second claim, although possible in principle, would be cumbersome. In Chapter 3, we will introduce some methods of determining the sizes of sets without actually counting sample points.
points in the case of three tosses of a die. The first statement can be verified by a direct counting of the elements of the sample space. Similar verification of the second claim, although possible in principle, would be cumbersome. In Chapter 3, we will introduce some methods of determining the sizes of sets without actually counting sample points.
Suppose that the only available information about the numbers, those that turn up on the upper faces of the die, is their sum. In such a case as outcomes, we take 11 possible values of the sum so that
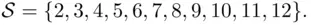
For instance, all outcomes on the diagonal of Table 1.1—(6, 1), (5, 2), (4, 3), (3, 4), (2, 5), and (1, 6)—are represented by the same value 7.
If we are interested in the number of accidents that occur at a given intersection within a month, the sample space might be taken as the set 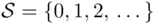 consisting of all nonnegative integers. Realistically, there is a practical limit, say
consisting of all nonnegative integers. Realistically, there is a practical limit, say 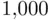 , of the monthly numbers of accidents at this particular intersection. Although one may think that it is simpler to take the sample space
, of the monthly numbers of accidents at this particular intersection. Although one may think that it is simpler to take the sample space 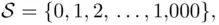 it turns out that it is often much simpler to take the infinite sample space if the “practical bound” is not very precise.
it turns out that it is often much simpler to take the infinite sample space if the “practical bound” is not very precise.
Читать дальше

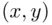 , with
, with 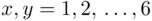 (see Table 1.1).
(see Table 1.1).
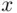
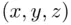 , with
, with 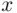 ,
, 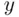 , and
, and 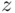 being integers between 1 and 6.
being integers between 1 and 6.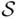 , is the set of all outcomes of an experiment. The elements of the sample space are called elementary outcomes, or sample points .
, is the set of all outcomes of an experiment. The elements of the sample space are called elementary outcomes, or sample points . has
has 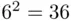 sample points in the case of two tosses, and
sample points in the case of two tosses, and 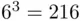 points in the case of three tosses of a die. The first statement can be verified by a direct counting of the elements of the sample space. Similar verification of the second claim, although possible in principle, would be cumbersome. In Chapter 3, we will introduce some methods of determining the sizes of sets without actually counting sample points.
points in the case of three tosses of a die. The first statement can be verified by a direct counting of the elements of the sample space. Similar verification of the second claim, although possible in principle, would be cumbersome. In Chapter 3, we will introduce some methods of determining the sizes of sets without actually counting sample points.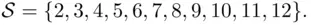
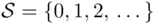 consisting of all nonnegative integers. Realistically, there is a practical limit, say
consisting of all nonnegative integers. Realistically, there is a practical limit, say 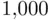 , of the monthly numbers of accidents at this particular intersection. Although one may think that it is simpler to take the sample space
, of the monthly numbers of accidents at this particular intersection. Although one may think that it is simpler to take the sample space 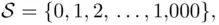 it turns out that it is often much simpler to take the infinite sample space if the “practical bound” is not very precise.
it turns out that it is often much simpler to take the infinite sample space if the “practical bound” is not very precise.










