of integration.Figure 6.2 Support of density
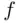
and the set
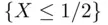
.Figure 6.3 A function that is not a cdf but satisfies (a)–(d).Figure 6.4 Marginal density.Figure 6.5 Condition for dependence.Figure 6.6 Probability of better of two attempts exceeding 0.75.Figure 6.7 Three‐component system.Figure 6.8 Joint distribution of
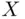
and
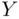
.Figure 6.9 Options for marginal densities of
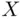
and
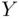
.Figure 6.10 Conditional densities.Figure 6.11 Triangular density.Figure 6.12 Supports of
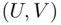
and
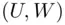
.Figure 6.13 Approximations of two conditioning events.Figure 6.14 First two generations in the process of grinding.
7 Chapter 7Figure 7.1 Interpretation of expected value of a discrete random variable.Figure 7.2 Interpretation of expected value of a continuous random variable....Figure 7.3 Approximating sums for Riemann and Lebesgue integrals.Figure 7.4 Graph of  and its cdf.Figure 7.5 Nonintegrable function whose iterated integrals exist and are not...Figure 7.6 Nonintegrable function whose iterated integrals exist and are equ...Figure 7.7 Length of 16 feet (Drawing by S. Niewiadomski).Figure 7.8 Two weightings of A and B.Figure 7.9 Dependent but uncorrelated random variables.
and its cdf.Figure 7.5 Nonintegrable function whose iterated integrals exist and are not...Figure 7.6 Nonintegrable function whose iterated integrals exist and are equ...Figure 7.7 Length of 16 feet (Drawing by S. Niewiadomski).Figure 7.8 Two weightings of A and B.Figure 7.9 Dependent but uncorrelated random variables.
8 Chapter 8Figure 8.1 Flowchart.Figure 8.2 Series system.Figure 8.3 Parallel system.Figure 8.4 Series‐parallel system.Figure 8.5 Flowchart.Figure 8.6 Two regression lines.Figure 8.7 Shapes of beta distributions.
9 Chapter 10Figure 10.1 Lifetime T(t*) of a bulb.
10 Chapter 11Figure 11.1 Likelihood function for the range  in uniform distribution.Figure 11.2 Likelihood function for five Bernoulli trials.
in uniform distribution.Figure 11.2 Likelihood function for five Bernoulli trials.
11 Chapter 12Figure 12.1 Power functions 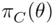 and
and 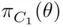 .Figure 12.2 Power functions of tests
.Figure 12.2 Power functions of tests 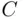 and
and 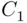 .Figure 12.3 Power of the two‐sided test
.Figure 12.3 Power of the two‐sided test 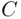 .Figure 12.4 Partition into sets
.Figure 12.4 Partition into sets 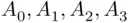 .Figure 12.5 Power functions of a one‐sided UMP test (dashed line) and a UMPU...Figure 12.6 Power function of an unbiased test.Figure 12.7 Golden rectangles.
.Figure 12.5 Power functions of a one‐sided UMP test (dashed line) and a UMPU...Figure 12.6 Power function of an unbiased test.Figure 12.7 Golden rectangles.
12 Chapter 13Figure 13.1 True regression.Figure 13.2 Linear regression for uniform distribution of 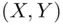 .Figure 13.3 Ages of Polish kings and their heirs at death.Figure 13.4 (a) No effects of
.Figure 13.3 Ages of Polish kings and their heirs at death.Figure 13.4 (a) No effects of 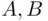 or
or 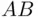 . (b) No effect of
. (b) No effect of 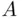 , effect of
, effect of 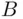 , no in...
, no in...
13 Chapter 16Figure 16.1 Posterior densities (dashed line) for different prior densities ...Figure 16.2 The 90% central credible interval (dotted line) and the 90% high...
14 1Figure A.1 The densities of BETA(2, 5), BETA(3, 3), and BETA(1, 4) distribut...Figure A.2 Histogram of the data generated from the BETA(2, 3) distribution ...Figure A.3 Histogram of the data generated from the BETA(2, 3) distribution ...
1 Wiley Series in Probability and Statistics Wiley Series in Probability and Statistics Established by Walter A. Shewhart and Samuel S. Wilks Editors: David J. Balding, Noel A. C. Cressie, Garrett M. Fitzmaurice, Geof H. Givens, Harvey Goldstein, Geert Molenberghs, David W. Scott, Adrian F. M. Smith, Ruey S. Tsay Editors Emeriti: J. Stuart Hunter, Iain M. Johnstone, Joseph B. Kadane, Jozef L. Teugels The Wiley Series in Probability and Statistics is well established and authoritative. It covers many topics of current research interest in both pure and applied statistics and probability theory. Written by leading statisticians and institutions, the titles span both state‐of‐the‐art developments in the field and classical methods. Reflecting the wide range of current research in statistics, the series encompasses applied, methodological and theoretical statistics, ranging from applications and new techniques made possible by advances in computerized practice to rigorous treatment of theoretical approaches. This series provides essential and invaluable reading for all statisticians, whether in academia, industry, government, or research. A complete list of titles in this series can be found at http://www.wiley.com/go/wsps
2 Title Page
3 Copyright
4 Dedication
5 Preface to Third Edition
6 Preface to Second Edition
7 About the Companion Website
8 Table of Contents
9 Begin Reading
10 APPENDIX A Supporting R Code
11 APPENDIX B Statistical Tables
12 Answers to Odd‐Numbered Problems
13 Index
14 WILEY END USER LICENSE AGREEMENT
1 ii
2 iv
3 v
4 xi
5 xii
6 xiii
7 xiv
8 xv
9 xvi
10 1
11 2
12 3
13 4
14 5
15 6
16 7
17 8
18 9
19 10
20 11
21 12
22 13
23 14
24 15
25 16
26 17
27 18
28 19
29 20
30 21
31 22
32 23
33 24
34 25
35 26
36 27
37 28
38 29
39 30
40 31
41 32
42 33
43 34
44 35
45 36
46 37
47 38
48 39
49 40
50 41
51 42
52 43
53 44
54 45
55 46
56 47
Читать дальше

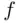 and the set
and the set 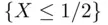 .Figure 6.3 A function that is not a cdf but satisfies (a)–(d).Figure 6.4 Marginal density.Figure 6.5 Condition for dependence.Figure 6.6 Probability of better of two attempts exceeding 0.75.Figure 6.7 Three‐component system.Figure 6.8 Joint distribution of
.Figure 6.3 A function that is not a cdf but satisfies (a)–(d).Figure 6.4 Marginal density.Figure 6.5 Condition for dependence.Figure 6.6 Probability of better of two attempts exceeding 0.75.Figure 6.7 Three‐component system.Figure 6.8 Joint distribution of 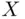 and
and 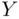 .Figure 6.9 Options for marginal densities of
.Figure 6.9 Options for marginal densities of 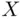 and
and 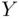 .Figure 6.10 Conditional densities.Figure 6.11 Triangular density.Figure 6.12 Supports of
.Figure 6.10 Conditional densities.Figure 6.11 Triangular density.Figure 6.12 Supports of 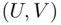 and
and 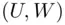 .Figure 6.13 Approximations of two conditioning events.Figure 6.14 First two generations in the process of grinding.
.Figure 6.13 Approximations of two conditioning events.Figure 6.14 First two generations in the process of grinding.
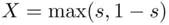 and its cdf.Figure 7.5 Nonintegrable function whose iterated integrals exist and are not...Figure 7.6 Nonintegrable function whose iterated integrals exist and are equ...Figure 7.7 Length of 16 feet (Drawing by S. Niewiadomski).Figure 7.8 Two weightings of A and B.Figure 7.9 Dependent but uncorrelated random variables.
and its cdf.Figure 7.5 Nonintegrable function whose iterated integrals exist and are not...Figure 7.6 Nonintegrable function whose iterated integrals exist and are equ...Figure 7.7 Length of 16 feet (Drawing by S. Niewiadomski).Figure 7.8 Two weightings of A and B.Figure 7.9 Dependent but uncorrelated random variables.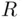 in uniform distribution.Figure 11.2 Likelihood function for five Bernoulli trials.
in uniform distribution.Figure 11.2 Likelihood function for five Bernoulli trials.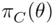 and
and 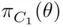 .Figure 12.2 Power functions of tests
.Figure 12.2 Power functions of tests  and
and  .Figure 12.3 Power of the two‐sided test
.Figure 12.3 Power of the two‐sided test  .Figure 12.4 Partition into sets
.Figure 12.4 Partition into sets 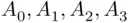 .Figure 12.5 Power functions of a one‐sided UMP test (dashed line) and a UMPU...Figure 12.6 Power function of an unbiased test.Figure 12.7 Golden rectangles.
.Figure 12.5 Power functions of a one‐sided UMP test (dashed line) and a UMPU...Figure 12.6 Power function of an unbiased test.Figure 12.7 Golden rectangles.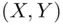 .Figure 13.3 Ages of Polish kings and their heirs at death.Figure 13.4 (a) No effects of
.Figure 13.3 Ages of Polish kings and their heirs at death.Figure 13.4 (a) No effects of 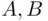 or
or 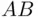 . (b) No effect of
. (b) No effect of 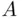 , effect of
, effect of 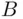 , no in...
, no in...










