Infinite operations on events play a very important role in the development of the theory, especially in determining limiting probabilities.
The definitions below will prepare the ground for the considerations in the following chapters. In Chapter 2, we will introduce probability as a number assigned to an event. Formally, we will be considering numerical functions defined on events, that is, on subsets of the sample space 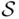 . As long as
. As long as 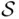 is finite or countably infinite, we can take the class of all subsets of
is finite or countably infinite, we can take the class of all subsets of 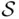 as the domain of definition of probability. In case of infinite but not countable
as the domain of definition of probability. In case of infinite but not countable 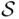 (e.g., where
(e.g., where 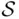 is an interval, the real line, or a plane), it may not be possible to define probability on the class of all subsets of
is an interval, the real line, or a plane), it may not be possible to define probability on the class of all subsets of 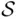 . Although the explanation lies beyond the scope of this book, we will show how the difficulties can be avoided by suitable restriction of the class of subsets of
. Although the explanation lies beyond the scope of this book, we will show how the difficulties can be avoided by suitable restriction of the class of subsets of 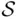 that are taken as events. We begin with the concept of closure under some operation.
that are taken as events. We begin with the concept of closure under some operation.
Definition 1.4.1We say that the class 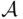 of subsets of
of subsets of 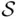 is closed under a given operation if the sets resulting from performing this operation on elements of
is closed under a given operation if the sets resulting from performing this operation on elements of 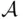 are also elements of
are also elements of 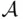 .
. 
Complementation 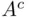 , finite union
, finite union 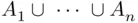 , infinite union
, infinite union 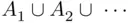 , limits of sequences
, limits of sequences 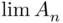 , are few examples of such operations.
, are few examples of such operations.
Let 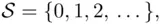 and let
and let 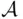 consist of all subsets of
consist of all subsets of 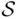 that are finite.
that are finite. 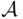 is closed under finite unions and all intersections, finite or not. Indeed, if
is closed under finite unions and all intersections, finite or not. Indeed, if  are finite sets, then
are finite sets, then 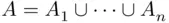 is also finite. Similarly, if
is also finite. Similarly, if 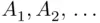 are finite, then
are finite, then 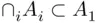 , and hence
, and hence 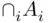 is also finite. However,
is also finite. However, 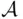 is not closed under complementation: if
is not closed under complementation: if 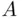 is finite (
is finite ( 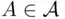 ), then
), then 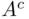 is not finite, and hence
is not finite, and hence 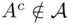 . On the other hand, if
. On the other hand, if 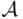 is the class of all subsets of
is the class of all subsets of 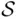 that contain some fixed element, say 0, then
that contain some fixed element, say 0, then 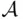 is closed under all intersections and unions, but it is not closed under complementation.
is closed under all intersections and unions, but it is not closed under complementation.
The following concepts have an important role in the theory of probability.
Definition 1.4.2A nonempty class 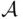 of subsets of
of subsets of 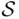 that is closed under complementation and all finite operations (i.e., finite union, finite intersection) is called a field . If
that is closed under complementation and all finite operations (i.e., finite union, finite intersection) is called a field . If 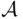 is closed under complementation and all countable operations, it is called a
is closed under complementation and all countable operations, it is called a 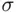 ‐ field . Finally, if
‐ field . Finally, if 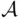 is closed under monotone passage to the limit, 4 it is called a monotone class .
is closed under monotone passage to the limit, 4 it is called a monotone class .
Let us observe that Definition 1.4.2 can be formulated in a more efficient way. For 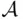 to be a field, it suffices to require that if
to be a field, it suffices to require that if 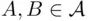 , then
, then 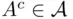 and
and 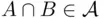 (or
(or 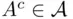 and
and 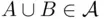 ). Any of these two conditions implies (by induction and De Morgan's laws) the closure of
). Any of these two conditions implies (by induction and De Morgan's laws) the closure of 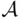 under all finite operations. Consequently, for
under all finite operations. Consequently, for 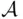 to be a
to be a 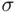 ‐field, it suffices to require that whenever
‐field, it suffices to require that whenever 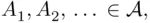 then
then 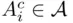 and
and 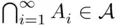 (or
(or 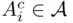 and
and 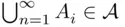 ); this follows again from De Morgan's laws. 5
); this follows again from De Morgan's laws. 5
Читать дальше

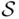 . As long as
. As long as  is finite or countably infinite, we can take the class of all subsets of
is finite or countably infinite, we can take the class of all subsets of 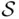 as the domain of definition of probability. In case of infinite but not countable
as the domain of definition of probability. In case of infinite but not countable 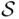 (e.g., where
(e.g., where 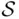 is an interval, the real line, or a plane), it may not be possible to define probability on the class of all subsets of
is an interval, the real line, or a plane), it may not be possible to define probability on the class of all subsets of 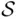 . Although the explanation lies beyond the scope of this book, we will show how the difficulties can be avoided by suitable restriction of the class of subsets of
. Although the explanation lies beyond the scope of this book, we will show how the difficulties can be avoided by suitable restriction of the class of subsets of 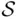 that are taken as events. We begin with the concept of closure under some operation.
that are taken as events. We begin with the concept of closure under some operation.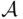 of subsets of
of subsets of 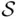 is closed under a given operation if the sets resulting from performing this operation on elements of
is closed under a given operation if the sets resulting from performing this operation on elements of 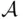 are also elements of
are also elements of 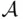 .
. 
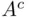 , finite union
, finite union 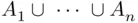 , infinite union
, infinite union 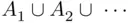 , limits of sequences
, limits of sequences 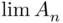 , are few examples of such operations.
, are few examples of such operations.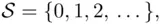 and let
and let 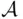 consist of all subsets of
consist of all subsets of 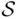 that are finite.
that are finite. 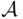 is closed under finite unions and all intersections, finite or not. Indeed, if
is closed under finite unions and all intersections, finite or not. Indeed, if  are finite sets, then
are finite sets, then 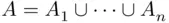 is also finite. Similarly, if
is also finite. Similarly, if 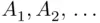 are finite, then
are finite, then 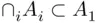 , and hence
, and hence 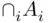 is also finite. However,
is also finite. However, 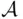 is not closed under complementation: if
is not closed under complementation: if 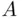 is finite (
is finite ( 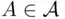 ), then
), then 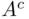 is not finite, and hence
is not finite, and hence 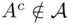 . On the other hand, if
. On the other hand, if 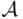 is the class of all subsets of
is the class of all subsets of 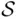 that contain some fixed element, say 0, then
that contain some fixed element, say 0, then 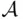 is closed under all intersections and unions, but it is not closed under complementation.
is closed under all intersections and unions, but it is not closed under complementation.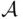 of subsets of
of subsets of 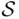 that is closed under complementation and all finite operations (i.e., finite union, finite intersection) is called a field . If
that is closed under complementation and all finite operations (i.e., finite union, finite intersection) is called a field . If 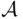 is closed under complementation and all countable operations, it is called a
is closed under complementation and all countable operations, it is called a 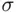 ‐ field . Finally, if
‐ field . Finally, if 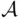 is closed under monotone passage to the limit, 4 it is called a monotone class .
is closed under monotone passage to the limit, 4 it is called a monotone class .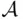 to be a field, it suffices to require that if
to be a field, it suffices to require that if 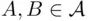 , then
, then 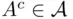 and
and 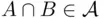 (or
(or 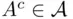 and
and 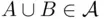 ). Any of these two conditions implies (by induction and De Morgan's laws) the closure of
). Any of these two conditions implies (by induction and De Morgan's laws) the closure of 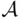 under all finite operations. Consequently, for
under all finite operations. Consequently, for 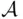 to be a
to be a 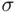 ‐field, it suffices to require that whenever
‐field, it suffices to require that whenever 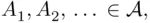 then
then 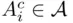 and
and 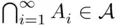 (or
(or 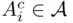 and
and 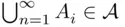 ); this follows again from De Morgan's laws. 5
); this follows again from De Morgan's laws. 5










