Robert Bartoszynski - Probability and Statistical Inference

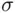The last in this series of concepts is that of the minimal field (or ‐field, or monotone class) containing a given set or collection of sets. We begin with some examples.

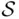Let be any set. On one extreme, the class consisting of two sets, 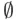and 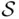, is closed under any operation so that 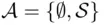is a field, a 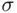‐field, and a monotone class. On the other extreme, the class of all subsets of 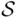is also closed under any operations, finite or not, and hence is a field, a 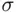‐field, and a monotone class. These two classes of subsets of 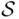form the smallest and the largest fields ( 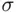‐field, monotone class).

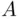For any event , it is easy to check that the class 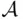, consisting of the four events 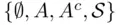, is closed under any operations: unions, intersections, and complements of members of 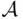are again members of 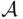. This class is an example of a field ( 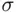‐field, monotone class) that contains the events 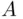and 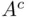, and it is the smallest such field ( 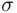‐field, monotone class).

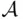On the other hand, the class , consisting of events 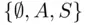, is a monotone class, but neither a field nor 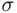‐field. If 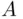and 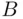are two events, then the smallest field 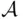containing 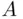and 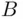must contain also the sets 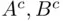, the intersections 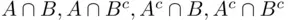, as well as their unions 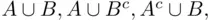and 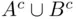. The closure property implies that unions such as 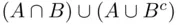, must also belong to .

We are now ready to present the final step.

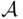Theorem 1.4.3 For any nonempty class of subsets of 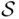, there exists a unique smallest field ( 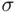‐field, monotone class) containing all sets in 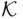. It is called the field ( 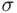‐field, monotone class) generated by .

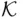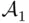Proof We will prove the assertion for fields. Observe first that if and 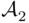are fields, then their intersection (i.e., the class of sets that belong to both 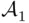and 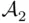) is also a field. For instance, if ( 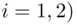, then because each 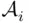is a field, and consequently 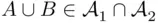. A similar argument holds for intersections and complements.