1 2.3.1 Label all statements below as true or false. (i) If is more likely to occur than , then . (ii) If occurs whenever does, then . (iii) If then whenever occurs, does also. (iv) If , then must occur three times out of every four. (v) The sum of probabilities of disjoint events and cannot exceed 1. (vi) If and are not disjoint, the sum of their probabilities exceeds 1. (vii) If and are all positive, then is also positive. (viii) If sample spaces for two experiments are identical, then the probability of the same event must be the same for both experiments.
2 2.3.2 A bathroom floor is covered by square tiles with side length . You drop a coin with diameter , where . Find: (i) The probability that the coin will rest entirely within one tile. (ii) The probability that the coin will partially cover four different tiles.
3 2.3.3 Show that first and third, as well as second and third, schemes of sampling chords (see Bertrand's paradox) are not equivalent.
2.4 Consequences of the Axioms
The simplest consequences of the axioms of probability are as follows:
1 The probability of the impossible event is zero: (2.1)This follows from the fact which is possible only if . It is important to realize that the converse is not true: the condition does not imply that . This is shown by the following example:Example 2.4Consider an experiment consisting of tossing a coin infinitely many times. The outcomes may be represented as infinite sequences of the form HHTHTTHT …so that the sample space contains infinitely many of such sequences. The event “heads only,” that is, the set consisting of just one sequence HHHH …, is not empty. However, the chance of such an outcome is, at least intuitively, zero: tails should come up sooner or later.
2 Probability is finitely additive:for any if the events are pairwise disjoint.In an infinite sequence events are pairwise disjoint only if are, so Axiom 3 applies. Therefore, using (2.1), we havewhile the left‐hand side is
3 Monotonicity: If then . This follows from the fact that . The events on the right‐hand side are disjoint, so we have by Axiom 1. Since for every event , we have
4 Probability is countably subadditive: (2.2)for every sequence of events This follows from representation ( 1.6) as a union of disjoint events, and then from monotonicity. We have
5 Complementation: (2.3)This follows from Axiom 2, by the fact that and are disjoint and .
6 Probability of a union of events: (2.4)Indeed, since , then . On the other hand, , and hence, . Solving for in one equation and substituting into the other, we obtain (2.4).
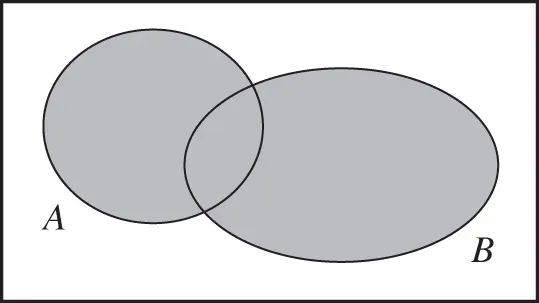
Figure 2.6Union of two events.
A more intuitive argument may be made by using Venn diagrams (see Figure 2.6). In the sum 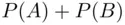 , each sample point from the intersection
, each sample point from the intersection  is included twice, so to obtain the probability of the union
is included twice, so to obtain the probability of the union  we must subtract the probability
we must subtract the probability 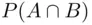 .
.
Suppose that 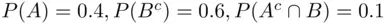 . Find
. Find  .
.
The best strategy for solving this kind of problem is finding the probabilities of all the intersections (in this case, 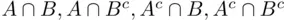 ). The probability
). The probability 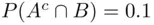 is given. Next,
is given. Next, 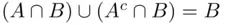 , and the events on the left are disjoint. So
, and the events on the left are disjoint. So 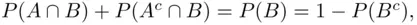 which means that
which means that 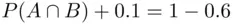 , and hence,
, and hence, 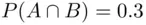 . Then, using
. Then, using 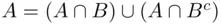 , we have
, we have 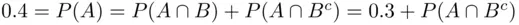 ; hence,
; hence, 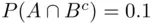 . similarly
. similarly 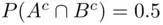 . Applying formula (2.3), we have
. Applying formula (2.3), we have 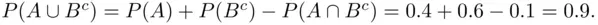
For the case of three events: 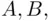 and
and 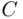 , the same argument based on Venn diagrams gives the formula
, the same argument based on Venn diagrams gives the formula
(2.5) 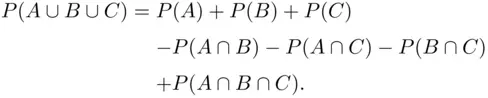
It can be checked at Figure 2.7that the formula ( 2.5) includes each part of the union 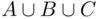 exactly once.
exactly once.
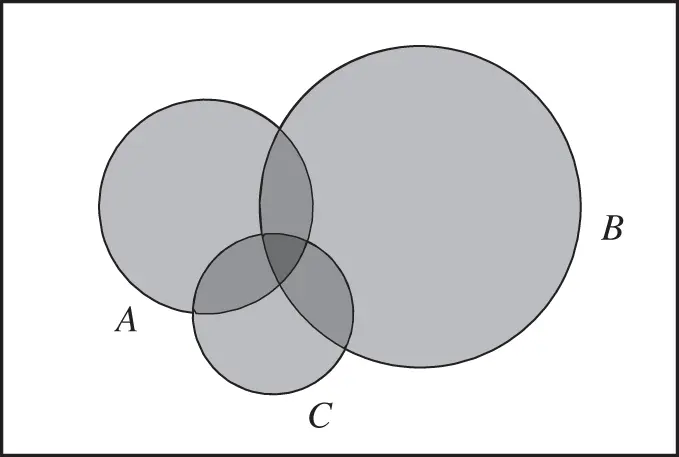
Figure 2.7Union of three events.
Formula ( 2.5) may be generalized to the case of the union of any finite number of events.
Theorem 2.4.1 For any events 
Читать дальше


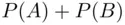 , each sample point from the intersection
, each sample point from the intersection  is included twice, so to obtain the probability of the union
is included twice, so to obtain the probability of the union  we must subtract the probability
we must subtract the probability 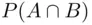 .
.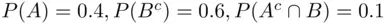 . Find
. Find  .
.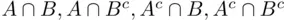 ). The probability
). The probability 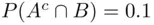 is given. Next,
is given. Next, 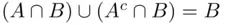 , and the events on the left are disjoint. So
, and the events on the left are disjoint. So 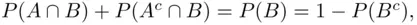 which means that
which means that 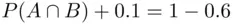 , and hence,
, and hence, 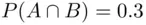 . Then, using
. Then, using 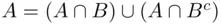 , we have
, we have 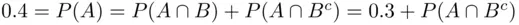 ; hence,
; hence, 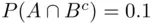 . similarly
. similarly 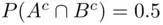 . Applying formula (2.3), we have
. Applying formula (2.3), we have 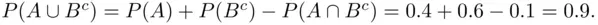
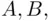 and
and 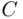 , the same argument based on Venn diagrams gives the formula
, the same argument based on Venn diagrams gives the formula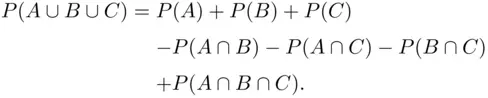
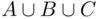 exactly once.
exactly once.












