A natural question arises: Are the three axioms of probability theory satisfied here (at least in their finite versions, without countable additivity)? On the one hand, this is the empirical question: The probabilities of various events can be determined numerically (for a given person), and then used to check whether the axioms hold. On the other hand, a superficial glance could lead one to conclude that there is no reason why person X's probabilities should obey any axioms: After all, subjective probabilities that do not satisfy probability axioms are not logically inconsistent.
However, there is a reason why a person's subjective probabilities should satisfy the axioms. For any axiom violated by the subjective probability of X (and X accepts the principle of SEU), one could design a bet that appears favorable to X (hence a bet that he will accept), but yet the bet is such that X is sure to lose.
Indeed, suppose first that the probability of some event 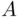 is negative. Consider the bet (lottery)
is negative. Consider the bet (lottery) 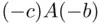 , (i.e., a lottery in which X pays the sum
, (i.e., a lottery in which X pays the sum 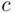 if
if 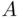 occurs and pays the sum
occurs and pays the sum 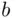 if
if  does not occur). We have here (identifying, for simplicity, the amounts of money with their utilities)
does not occur). We have here (identifying, for simplicity, the amounts of money with their utilities)
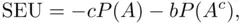
so that SEU is positive for a large enough 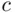 if
if 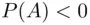 . Thus, following the principle of maximizing SEU, X should accept this lottery over the status quo (no bet), but he will lose in any case—the amount
. Thus, following the principle of maximizing SEU, X should accept this lottery over the status quo (no bet), but he will lose in any case—the amount 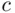 or the amount
or the amount  .
.
Suppose now that 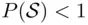 . Consider the bet
. Consider the bet 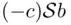 whose SEU is
whose SEU is 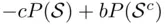 . Since
. Since 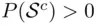 , making
, making 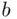 large enough, the bet appears favorable to X, yet he is bound to lose the amount
large enough, the bet appears favorable to X, yet he is bound to lose the amount 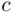 on every trial.
on every trial.
If 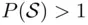 or if the additivity axiom is not satisfied, one can also design bets that will formally be favorable for X (SEU will be positive) but that X will be bound to lose. Determination of these bets is left to the reader.
or if the additivity axiom is not satisfied, one can also design bets that will formally be favorable for X (SEU will be positive) but that X will be bound to lose. Determination of these bets is left to the reader.
1 2.7.1 Peter and Tom attend the same college. One day Tom buys a ticket for a rock concert. Tickets are already sold out and are in great demand. Peter, who does not have a ticket, agrees to play the following game with Tom. For a fee of $25, Peter will toss a coin three times and receive the ticket if all tosses show up heads. Otherwise, for an additional fee of $50, Peter will toss a coin two more times and receive the ticket if both tosses show up heads. If not, then for an additional fee of $100, Peter will toss a coin and receive the ticket if the toss shows up heads. Otherwise, all money will be given to Tom, and he also will keep the ticket. Assuming that the coin is fair, subjective probabilities of various outcomes coincide with objective probabilities, and that Peter's utility is linear in money, show that Peter's utility of the ticket exceeds $200.
2 2.7.2 Refer to Problem 2.7.1. Tom would agree on the following conditions: Peter pays him $50 and tosses a coin, winning the ticket if it comes up heads, and otherwise losing $50. In such a situation, should they both agree that Peter buys the ticket from Tom for $150?
3 2.7.3 Suppose that Tom is confronted with the choice between two options: , which is simply to receive $1,000,000, or , which is to receive $5,000,000 with probability 0.1, receive $1,000,000 with probability 0.89, and receive $0 with the remaining probability 0.01. After some deliberation, Tom decides that is better, mostly because the outcome $0, unlikely as it may be, is very unattractive.Tom is also confronted with a choice between two other options, and . In , he would receive $5,000,000 with probability 0.1 and $0 with probability 0.9. In , he would receive $1,000,000 with probability 0.11 and $0 with probability 0.89. Here Tom prefers : the “unattractive” option $0 has about the same probability in both and , while the positive outcome, although slightly less probable under , is much more desirable in that in . Show that these preferences of Tom are not compatible with the assumption that he has utilities and of $5,000,000, $1,000,000, and $0, such that (This is known as Allais' paradox; Allais, 1953).
1 1The nature of the class of all events will be (to a certain extent) explicated in Section 2.6. See also Section 1.4.
Chapter 3 Counting
3.1 Introduction
In the classical interpretation of probability, all outcomes of the experiment are equally likely, and the probability of an event is obtained as the relative frequency of outcomes that favor this event (imply its occurrence). Simple enumeration of elements in these sets is often not feasible, and therefore practical implementation of this principle requires developing techniques for counting elements of certain sets (e.g., sets of all possible outcomes of an experiment). The branch of mathematics dealing with such methods is called combinatorics , or combinatorial analysis . In this chapter, we introduce some combinatorial principles and illustrate their use in computing probabilities.
Читать дальше

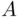 is negative. Consider the bet (lottery)
is negative. Consider the bet (lottery) 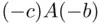 , (i.e., a lottery in which X pays the sum
, (i.e., a lottery in which X pays the sum 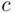 if
if 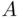 occurs and pays the sum
occurs and pays the sum 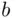 if
if  does not occur). We have here (identifying, for simplicity, the amounts of money with their utilities)
does not occur). We have here (identifying, for simplicity, the amounts of money with their utilities)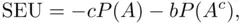
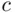 if
if 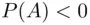 . Thus, following the principle of maximizing SEU, X should accept this lottery over the status quo (no bet), but he will lose in any case—the amount
. Thus, following the principle of maximizing SEU, X should accept this lottery over the status quo (no bet), but he will lose in any case—the amount 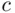 or the amount
or the amount  .
.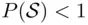 . Consider the bet
. Consider the bet 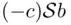 whose SEU is
whose SEU is 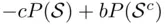 . Since
. Since 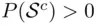 , making
, making 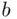 large enough, the bet appears favorable to X, yet he is bound to lose the amount
large enough, the bet appears favorable to X, yet he is bound to lose the amount 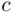 on every trial.
on every trial.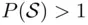 or if the additivity axiom is not satisfied, one can also design bets that will formally be favorable for X (SEU will be positive) but that X will be bound to lose. Determination of these bets is left to the reader.
or if the additivity axiom is not satisfied, one can also design bets that will formally be favorable for X (SEU will be positive) but that X will be bound to lose. Determination of these bets is left to the reader.










