Corollary 3.2.4 The number of ordered pairs 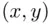 with
with 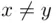 that can be formed out of
that can be formed out of 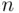 distinct elements of a set of size
distinct elements of a set of size 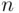 is
is 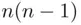 .
.
Instead of thinking in terms of operations, we can still use Cartesian products here. Thus, 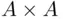 has
has 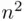 elements by Theorem 3.2.3, of which
elements by Theorem 3.2.3, of which 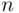 are of the form
are of the form  . The number of pairs with elements distinct is
. The number of pairs with elements distinct is 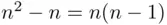 .
.
We can generalize these considerations as follows:
Definition 3.2.1An ordered sequence of 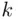 elements selected without replacement from a set of
elements selected without replacement from a set of 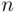 distinct elements
distinct elements 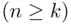 is called a permutation of
is called a permutation of 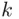 out of
out of 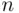 elements.
elements.
Theorem 3.2.5 The number of permutations of 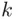 out of
out of 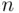 , denoted
, denoted 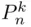 , equals
, equals
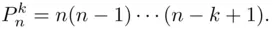
Proof : The argument here repeatedly uses the “operation” principle: the first choice can be made in 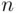 ways, the second in
ways, the second in  ways, the
ways, the 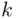 th in
th in 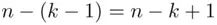 ways.
ways.
If 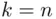 , consecutive choices form an ordering of the entire set of size
, consecutive choices form an ordering of the entire set of size 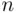 . We obtain the following:
. We obtain the following:
Corollary 3.2.6 The set of 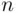 elements can be ordered in
elements can be ordered in
(3.2) 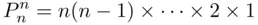
distinct ways.
The product ( 3.2) occurs often and has a special symbol:

to be read “ 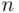 factorial.” We have therefore
factorial.” We have therefore
(3.3) 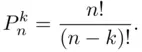
For a reason that will become apparent later, we adopt the convention
(3.4) 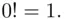
The letters I, I, I, I, M, P, P, S, S, S, S are arranged at random. What is the probability that the arrangement will spell MISSISSIPPI?
We can solve this problem treating the choices of consecutive letters as “operations.” The first operation must give the letter M; hence, there is only one way of choosing it. The next letter (out of the remaining 10) must be an I, and it can be selected in four ways. Proceeding in this way, the sequence of consecutive 11 choices leading to the word MISSISSIPPI can be performed in  ways, which equals
ways, which equals 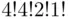 . On the other hand, the total number of ways one can perform the operations of consecutively choosing letters from the set is
. On the other hand, the total number of ways one can perform the operations of consecutively choosing letters from the set is 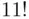 . Consequently, the required probability equals
. Consequently, the required probability equals
(3.5) 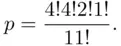
In this solution, the letters are regarded as distinguishable, as if we had four letters  , labeled
, labeled 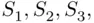 and
and 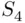 , and similarly for the other letters. In this case, the numerator and denominator are, respectively, the number of ways one can order the set of distinguishable letters so as to form the word MISSISSIPPI and the total number of orderings. Alternatively, one can regard the identical letters as indistinguishable, and in this case, we have only one way of ordering them so as to spell the required word, and a total of
, and similarly for the other letters. In this case, the numerator and denominator are, respectively, the number of ways one can order the set of distinguishable letters so as to form the word MISSISSIPPI and the total number of orderings. Alternatively, one can regard the identical letters as indistinguishable, and in this case, we have only one way of ordering them so as to spell the required word, and a total of 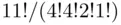 distinguishable ways of ordering these letters. Indeed, the denominator here represents the number of ways of permuting letters so as to leave the arrangement invariant. Now,
distinguishable ways of ordering these letters. Indeed, the denominator here represents the number of ways of permuting letters so as to leave the arrangement invariant. Now,
Читать дальше

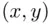 with
with 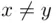 that can be formed out of
that can be formed out of 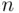 distinct elements of a set of size
distinct elements of a set of size 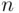 is
is 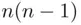 .
.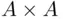 has
has 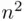 elements by Theorem 3.2.3, of which
elements by Theorem 3.2.3, of which 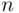 are of the form
are of the form  . The number of pairs with elements distinct is
. The number of pairs with elements distinct is 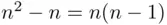 .
.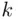 elements selected without replacement from a set of
elements selected without replacement from a set of 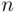 distinct elements
distinct elements 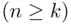 is called a permutation of
is called a permutation of 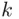 out of
out of 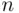 elements.
elements.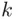 out of
out of 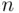 , denoted
, denoted 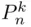 , equals
, equals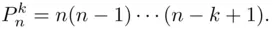
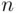 ways, the second in
ways, the second in  ways, the
ways, the 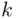 th in
th in 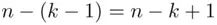 ways.
ways.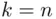 , consecutive choices form an ordering of the entire set of size
, consecutive choices form an ordering of the entire set of size 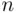 . We obtain the following:
. We obtain the following: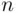 elements can be ordered in
elements can be ordered in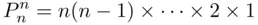

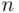 factorial.” We have therefore
factorial.” We have therefore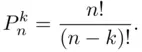
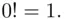
 ways, which equals
ways, which equals 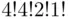 . On the other hand, the total number of ways one can perform the operations of consecutively choosing letters from the set is
. On the other hand, the total number of ways one can perform the operations of consecutively choosing letters from the set is 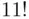 . Consequently, the required probability equals
. Consequently, the required probability equals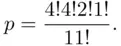
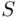 , labeled
, labeled 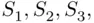 and
and 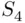 , and similarly for the other letters. In this case, the numerator and denominator are, respectively, the number of ways one can order the set of distinguishable letters so as to form the word MISSISSIPPI and the total number of orderings. Alternatively, one can regard the identical letters as indistinguishable, and in this case, we have only one way of ordering them so as to spell the required word, and a total of
, and similarly for the other letters. In this case, the numerator and denominator are, respectively, the number of ways one can order the set of distinguishable letters so as to form the word MISSISSIPPI and the total number of orderings. Alternatively, one can regard the identical letters as indistinguishable, and in this case, we have only one way of ordering them so as to spell the required word, and a total of 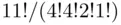 distinguishable ways of ordering these letters. Indeed, the denominator here represents the number of ways of permuting letters so as to leave the arrangement invariant. Now,
distinguishable ways of ordering these letters. Indeed, the denominator here represents the number of ways of permuting letters so as to leave the arrangement invariant. Now,










