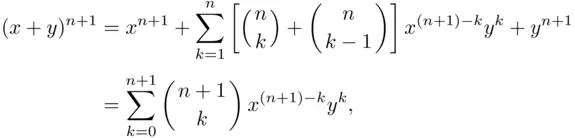(3.13) 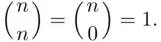
We will now study some properties of the binomial coefficients 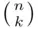 . First,
. First,
(3.14) 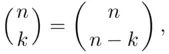
which follows from the symmetry in formula ( 3.10). One can also prove ( 3.14) by observing that choosing a set of size 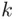 is equivalent to “leaving out” a set of size
is equivalent to “leaving out” a set of size  . The number of different sets of size
. The number of different sets of size 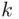 chosen must be equal to the number of different sets of size
chosen must be equal to the number of different sets of size  “chosen” by leaving them out.
“chosen” by leaving them out.
We will now prove the following theorem:
Theorem 3.3.2 (Pascal's Triangle) The binomial coefficients satisfy the relation
(3.15) 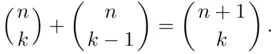
Proof : The formula can be easily proved by expressing the left‐hand side using ( 3.8) and reducing it algebraically to get the right‐hand side. It is, however, more instructive to rely on the interpretation of the coefficients 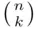 as
as 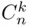 . The right‐hand side of ( 3.15) counts the number of sets of size
. The right‐hand side of ( 3.15) counts the number of sets of size 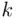 that can be chosen out of a set of size
that can be chosen out of a set of size 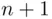 . Let us take one element of the latter set and label it somehow. We have then a set of
. Let us take one element of the latter set and label it somehow. We have then a set of 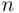 unlabeled and
unlabeled and 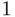 labeled element. Each subset of size
labeled element. Each subset of size 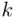 is one of the following two categories: (1) subsets that contain only
is one of the following two categories: (1) subsets that contain only 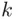 unlabeled elements, or (2) subsets that contain
unlabeled elements, or (2) subsets that contain  unlabeled elements and one labeled element. The two terms on the left‐hand side of ( 3.15) count the numbers of subsets of the first category and of the second category.
unlabeled elements and one labeled element. The two terms on the left‐hand side of ( 3.15) count the numbers of subsets of the first category and of the second category.
The name Pascal's triangle reflects a way of obtaining the coefficients 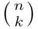 . We build Pascal's triangle starting with the top row (counted as the zeroth row), which consists of the single number 1 (see Figure 3.1). Then we obtain each number in the subsequent rows as a sum of two numbers directly above it (as marked with arrows in the fifth row). The consecutive numbers in the
. We build Pascal's triangle starting with the top row (counted as the zeroth row), which consists of the single number 1 (see Figure 3.1). Then we obtain each number in the subsequent rows as a sum of two numbers directly above it (as marked with arrows in the fifth row). The consecutive numbers in the 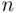 th row are, reading from the left, the values of
th row are, reading from the left, the values of
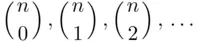
so that, for example, 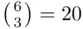 , as marked on the triangle in Figure 3.1. While the Pascal triangle was very useful in the past, today it is of a historical value as statistical packages are used to obtain values of binomial coefficients.
, as marked on the triangle in Figure 3.1. While the Pascal triangle was very useful in the past, today it is of a historical value as statistical packages are used to obtain values of binomial coefficients.
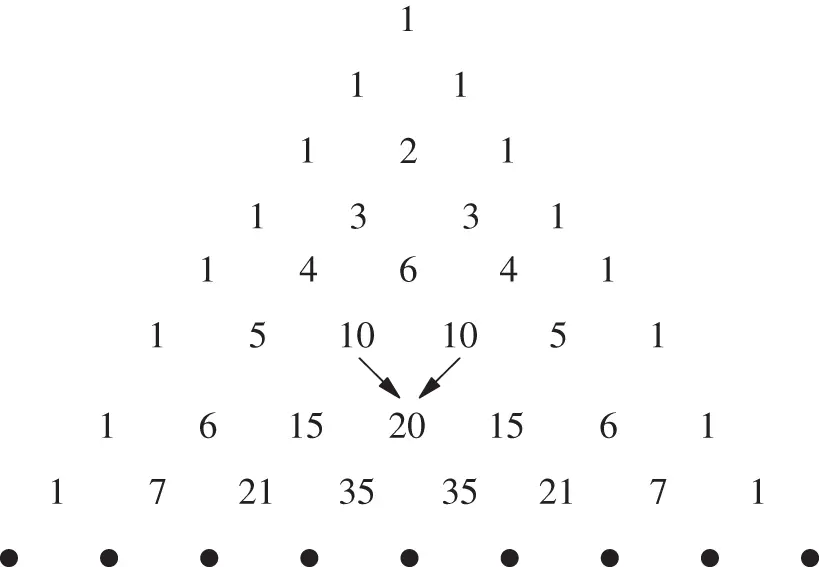
Figure 3.1Pascal's triangle.
The name binomial coefficient is connected to the following formula:
Theorem 3.3.3 (Newton's Binomial Formula) For any positive integer 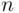 and real
and real 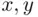 , we have
, we have
(3.16) 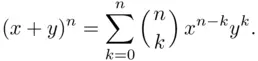
Proof : We will prove the theorem by induction. For 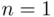 , the right‐hand side equals
, the right‐hand side equals 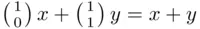 . Assume now that the assertion holds for some
. Assume now that the assertion holds for some 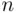 , and multiply both sides of ( 3.16) by
, and multiply both sides of ( 3.16) by 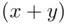 . Then
. Then
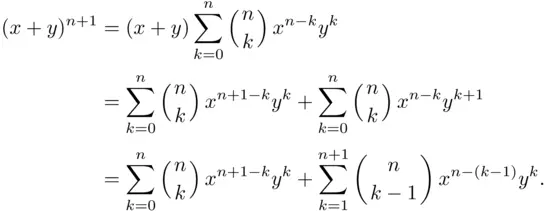
Separating the term for  in the first sum, and the term for
in the first sum, and the term for 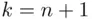 in the last sum, we may write
in the last sum, we may write
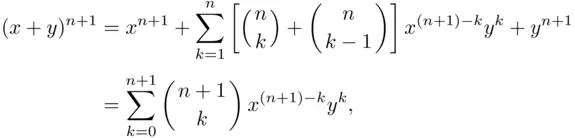
where the last equality is due to Theorem 3.3.2.
Читать дальше

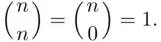
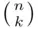 . First,
. First,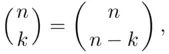
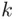 is equivalent to “leaving out” a set of size
is equivalent to “leaving out” a set of size  . The number of different sets of size
. The number of different sets of size 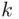 chosen must be equal to the number of different sets of size
chosen must be equal to the number of different sets of size  “chosen” by leaving them out.
“chosen” by leaving them out.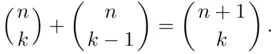
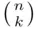 as
as 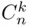 . The right‐hand side of ( 3.15) counts the number of sets of size
. The right‐hand side of ( 3.15) counts the number of sets of size 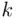 that can be chosen out of a set of size
that can be chosen out of a set of size 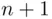 . Let us take one element of the latter set and label it somehow. We have then a set of
. Let us take one element of the latter set and label it somehow. We have then a set of 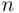 unlabeled and
unlabeled and 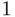 labeled element. Each subset of size
labeled element. Each subset of size 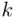 is one of the following two categories: (1) subsets that contain only
is one of the following two categories: (1) subsets that contain only 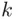 unlabeled elements, or (2) subsets that contain
unlabeled elements, or (2) subsets that contain  unlabeled elements and one labeled element. The two terms on the left‐hand side of ( 3.15) count the numbers of subsets of the first category and of the second category.
unlabeled elements and one labeled element. The two terms on the left‐hand side of ( 3.15) count the numbers of subsets of the first category and of the second category.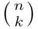 . We build Pascal's triangle starting with the top row (counted as the zeroth row), which consists of the single number 1 (see Figure 3.1). Then we obtain each number in the subsequent rows as a sum of two numbers directly above it (as marked with arrows in the fifth row). The consecutive numbers in the
. We build Pascal's triangle starting with the top row (counted as the zeroth row), which consists of the single number 1 (see Figure 3.1). Then we obtain each number in the subsequent rows as a sum of two numbers directly above it (as marked with arrows in the fifth row). The consecutive numbers in the 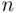 th row are, reading from the left, the values of
th row are, reading from the left, the values of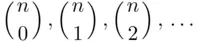
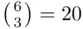 , as marked on the triangle in Figure 3.1. While the Pascal triangle was very useful in the past, today it is of a historical value as statistical packages are used to obtain values of binomial coefficients.
, as marked on the triangle in Figure 3.1. While the Pascal triangle was very useful in the past, today it is of a historical value as statistical packages are used to obtain values of binomial coefficients.
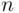 and real
and real 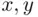 , we have
, we have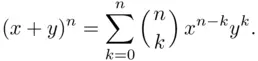
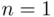 , the right‐hand side equals
, the right‐hand side equals 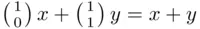 . Assume now that the assertion holds for some
. Assume now that the assertion holds for some 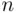 , and multiply both sides of ( 3.16) by
, and multiply both sides of ( 3.16) by 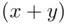 . Then
. Then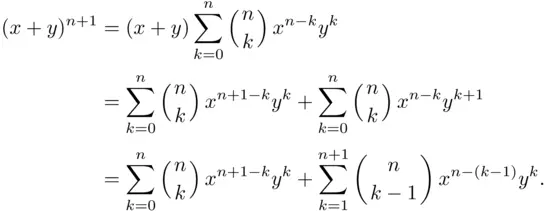
 in the first sum, and the term for
in the first sum, and the term for 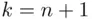 in the last sum, we may write
in the last sum, we may write