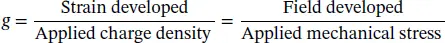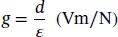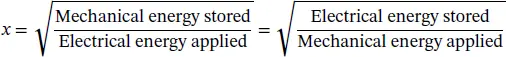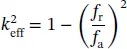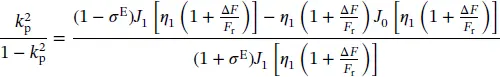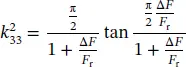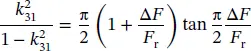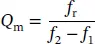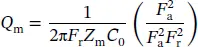(1.8) 
The g ‐constants are calculated from the piezoelectric charge (strain) constant ( d ) and relative permittivity ( ε ) from the equation:
(1.9) 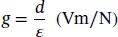
Depending on the type of relative directions, the g constant can be categorized as g 33, g 31, or g 15, corresponding to d 33, d 31, or d 15, respectively.
1.4.2 Piezoelectric Coupling Coefficient
The piezoelectric coupling coefficient (sometimes referred as the electromechanical coupling coefficient) is defined as the ratio of the mechanical energy accumulated in response to an electrical input or vice versa. It also corresponds to the fraction of electrical energy that can be converted into mechanical energy and vice versa. Thus, the piezoelectric coupling coefficient can be expressed by the following equation:
(1.10) 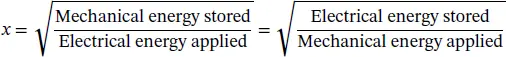
The coupling factor can be calculated based on the measured resonance and anti‐resonance frequencies of a piezoelectric element, depending on the vibration mode at which the element is excited. The most used coupling factors are k pand k tfor the vibration along the radial and thickness directions in a circle‐shaped disk, respectively. In general, a useful parameter k effis frequently used to express the effective coupling coefficient of an resonator with an arbitrary shape, either at its fundamental resonance or at any overtone modes, and is expressed as follows:
(1.11) 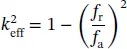
where f rand f astand for resonating frequency and anti‐resonating frequency, respectively. The coupling coefficients can be calculated for the various modes of vibration from the following equations:
(1.12) 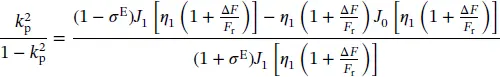
where
| J |
Bessel function of the first kind and zero order |
| J 1 |
Bessel function of the first kind and first order |
| σ E |
Poisson's ratio |
| η 1 |
Lowest positive root of (1 + σ E)· J 1 η = ηJ 0( η ) |
| F r |
Resonance frequency (Hz) |
| F a |
Anti‐resonance frequency (Hz) |
| Δ F |
= F a− F r(Hz) |
Assuming that σ E= 0.31 for PZT ceramics and η 1= 2.05, the following simplified equations holds:
(1.13) 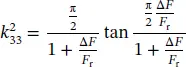
(1.14) 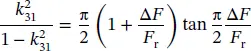
1.4.3 Mechanical Quality Factor
The mechanical Q (also referred to as Q ) is the ratio of the reactance to the resistance in the series equivalent circuit representing the piezoelectric resonator, which is related to the sharpness of the resonance frequency. The mechanical Q Mcan be calculated using the equation:
(1.15) 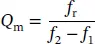
where f ris the resonance frequency, f 1and f 2are frequencies at −3 dB of the maximum admittance. The mechanical Q Mis also related to the electromechanical coupling factor k , following the equation:
(1.16) 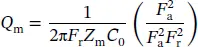
where
| F r |
Resonance frequency (Hz) |
| F a |
Anti‐resonance frequency (Hz) |
| Z m |
Impedance at F r(ohm) |
| C 0 |
Static capacitance (Farad) |
1.5 Issues for Measuring Piezoelectric Properties
1.5.1 Measurement of Direct Piezoelectric Coefficient Using the Berlincourt Method
One of the most crucial figures of merits characterizing a piezoelectric material is the piezoelectric charge constant, also called the direct piezoelectric coefficient. It reflects the internal generation of electrical charges resulting from an applied mechanical force, as previously mentioned. Basically, the higher the piezoelectric charge constant, the more active a piezoelectric material is. A fast and accurate evaluation of the direct piezoelectric coefficient can be realized by the Berlincourt method associated with a quasi‐static piezo d 33‐meter [6, 28–31]. In this method, sample size or geometric shape becomes a factor that need not be strictly taken into account. Besides, the availability and convenient operation of a d 33‐meter are obvious, which make it a predominantly used method in practice. However, the name of “Berlincourt method” is often mistaken by some people nowadays as being synonymous with the quasi‐static measurements of the direct piezoelectric coefficient. The latter more broadly refers to the methods operating at low or quasi‐static frequencies, and its basic principle of was proposed in “Piezoelectric Ceramics” by Jaffe et al. The name of “Berlincourt” actually derives from the researcher, Don Berlincourt, who devoted a lot of effort to the development of the initial commercial d 33apparatus based on the quasi‐static measurement principle [28].
Here, we consider a simple case of measuring the d 33value of a ceramic sample poled along the three‐direction ( z ) to elucidate the mathematical basis for the Berlincourt method. In the common case, the interaction between the mechanical and electrical behavior can be described by the equation d 33= [ δD 3 /δT 3] E, where D 3denotes electric displacement along the three‐direction ( z ) and T 3denotes applied stress also along the three‐direction ( z ). For the practical measurement of d 33, this equation can be altered as d 33= [( Q / A )⋯( F / A )] = ( Q / F ), where F is applied force, A is the acting area, and Q is charge developed. It is obvious that d 33can be determined via measuring the charge induced by a certain force applied on the piezoelectric samples, while the measurement of the areas can be neglected as they cancel out. It should be noted that a constant electric field as fulfilled in the short‐circuit condition is the prerequisite of this measurement. To achieve this condition, a large capacitor across the Device Under Test (DUT) or a virtual‐ground amplifier is often embedded in the test system.
Читать дальше