1 Cover
2 Title Page Multiscale Modelling and Optimisation of Materials and Structures Tadeusz Burczyński Institute of Fundamental Technological Research Polish Academy of Sciences Warszawa, Poland Maciej Pietrzyk AGH University of Science and Technology Kraków, Poland Wacław Kuś Silesian University of Technology Gliwice, Poland Łukasz Madej AGH University of Science and Technology Kraków, Poland Adam Mrozek AGH University of Science and Technology Kraków, Poland Łukasz Rauch AGH University of Science and Technology Kraków, Poland
3 Copyright Page
4 Preface
5 Biography
6 1 Introduction to Multiscale Modelling and Optimization 1.1 Multiscale Modelling 1.2 Optimization 1.3 Contents of the Book References
7 2 Modelling of Phenomena 2.1 Physical Phenomena in Nanoscale 2.2 Physical Phenomena in Microscale References
8 3 Computational Methods 3.1 Computational Methods for Continuum 3.2 Computational Methods for Nano and Micro 3.3 Methods of Optimization References
9 4 Preparation of Material Representation 4.1 Generation of Nanostructures 4.2 Microstructure References
10 5 Examples of Multiscale Simulations 5.1 Classification of Multiscale Modelling Methods 5.2 Case Studies References
11 6 Optimization and Identification in Multiscale Modelling 6.1 Multiscale Optimization 6.2 Identification in Multiscale Modelling References
12 7 Computer Implementation Issues7.1 Interactions Between the Analysis and Optimization Solutions 7.2 Visualization of Large Data Sets References
13 8 Concluding Remarks
14 Index
15 End User License Agreement
1 Chapter 2 Table 2.1 Computational times of the SLMoS 2MD simulation with different at... Table 2.2 Chemical compositions of investigated steels. Table 2.3 Coefficients in Eq. (2.60) obtained from the inverse analysis for... Table 2.4Coefficients in Eq. (2.61) obtained from the inverse analysis for ... Table 2.5 Coefficients in Eq. (2.62) obtained from the inverse analysis for... Table 2.6 Coefficients in Eqs. (2.63)–(2.68) obtained from the inverse anal... Table 2.7 Coefficients in Eq. (2.60) obtained from the inverse analysis for... Table 2.8 Coefficients in Eqs. (2.69) and (2.71) describing the kinetics of... Table 2.9 Coefficients in Eq. (2.72) describing the recrystallized grain si... Table 2.10 Coefficients in Eq. (2.16) describing the critical strain for dy... Table 2.11 Coefficients in Eq. (2.74) describing kinetics of dynamic recrys... Table 2.12 Coefficients in Eq. (2.75) describing a grain size after dynamic...Table 2.13 Coefficients in Eq. (2.76) describing kinetics of metadynamic re...Table 2.14 Coefficients in Eq. (2.77) describing a grain size after metadyn...Table 2.15 Coefficients in Eq. (2.78) describing a grain growth.Table 2.16 Coefficients in Eq. (2.79) describing a grain growth.Table 2.17 Equations describing recrystallization and precipitation times f...Table 2.18 Additional equations in the model.Table 2.19 Equations describing parameters in model B.Table 2.20 Coefficients in the phase transformation model determined using ...
2 Chapter 3Table 3.1 Coefficient θ and matrices  and
and 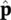 for various integration s...
for various integration s...
3 Chapter 4Table 4.1 Number of boundary elements of the continuum models. The elastic ...
4 Chapter 5Table 5.1 A number of boundary elements of the continuum models.Table 5.2 Displacements of the selected atoms.
5 Chapter 6Table 6.1 Parameters of the Murrell‐Mottram potential for Al.Table 6.2 Lowest energies of the Morse and Murrell‐Mottram clusters.Table 6.3 Constraints imposed on design variables.Table 6.4 Parameters of optimization algorithms.Table 6.5 Results of optimization.Table 6.6 Values of design variables.Table 6.7 Results of material parameters identification.Table 6.8 The material properties for the microscale.Table 6.9 The evolutionary algorithm parameters.Table 6.10 The results of identification.Table 6.11 Results of identification for Variant 1.Table 6.12 Numerical results of identification for Variants 2–5.
6 Chapter 7Table 7.1 A number of points for spheres in Figure 7.9.Table 7.2 Result of tests for a gain of memory during nanostructure visuali...Table 7.3 FPS obtained for various data sizes (less than two million partic...Table 7.4 FPS obtained for various data sizes (large sets with more than tw...Table 7.5 Computing time depending on the number of threads.Table 7.6 Profiling of the whole algorithm for the subsequent tasks of the ...
1 Chapter 1 Figure 1.1 Multiscale concept diagram which illustrates ‘macro’, ‘meso’, ‘mi... Figure 1.2 Illustration of computational homogenization concept. Figure 1.3 (a) Internal variable method as a precursor of upscaling and (b) t...
2 Chapter 2 Figure 2.1 The Lennard‐Jones atomic potential and force. Figure 2.2 The Morse potential. Figure 2.3 Typical material responses to plastic deformation. Figure 2.4 Schematic illustration of FE model application for a prediction o... Figure 2.5 Schematic illustrations of selected plastometric tests. Figure 2.6 Selected examples of comparison of loads recorded for the two DP ... Figure 2.7 Microstructures at various stages of recrystallization.Figure 2.8 Flow chart of calculations of microstructure evolution in microal...Figure 2.9 Classification of selected phase transformation models: computing...Figure 2.10 Comparison of the CCT diagrams obtained from measurements (fille...Figure 2.11 Comparison of the CCT diagrams (a) and volume fractions of phase...Figure 2.12 Comparison of the CCT diagrams obtained from measurements (fille...Figure 2.13 Thermal profile (dotted line) and changes of volume fractions of...Figure 2.14 Thermal profile (dotted line) and changes of volume fractions of...Figure 2.15 Transcrystalline fracture (a) and intercrystalline fracture (b)....Figure 2.16 Ductile and brittle material behaviour.Figure 2.17 Interpretation of the J integral.Figure 2.18 Schematic illustration of the RVE approach based on homogenizati...Figure 2.19 Geometric measure of damages proposed by Kachanov [46] for mater...Figure 2.20 Macroscopic features of damages proposed by Chaboche for materia...Figure 2.21 Mechanical models of ideal elastic (a) and ideal viscous (b) mat...Figure 2.22 Kelvin (a) and Maxwell (b) material rheological models.Figure 2.23 Typical creep curve with marked first (I), second (II), and thir...Figure 2.24 Schematic relation between loading stress and the time to damage...
3 Chapter 3Figure 3.1 Representation of a 2D domain by a collection of triangles and qu...Figure 3.2 Discontinuity path (a) and domains (b) created in [86].Figure 3.3 Illustration of the displacement field decomposition [86].Figure 3.4 Illustration of the finite element approximation [86].Figure 3.5 Illustration of the unit jump function finite element approximati...Figure 3.6 The elastic body bounded by the boundary.Figure 3.7 An area near the boundary of the body.Figure 3.8 Discretization with boundary elements.Figure 3.9 A body discretized using finite and boundary elements.Figure 3.10 The infinite body discretized using finite and boundary elements...Figure 3.11 Homogenization of the non‐homogeneous structure.Figure 3.12 Models of a structure with locally periodical microstructures: (...Figure 3.13 Computational homogenization scheme: the average strain and stre...Figure 3.14 Rupture of the SLMoS 2lattice during the tensile test along the ...Figure 3.15 Stress–strain relation of the SLMoS 2lattice obtained in armchai...Figure 3.16 Illustration of the cutoff radius and the ‘skin’ parameter.Figure 3.17 Illustration of the periodic boundary conditions.Figure 3.18 The reflecting wall.Figure 3.19 Rectangular plate with a crack under tensile load. A constant li...Figure 3.20 Results (a), (b), and (c) after, respectively, 6, 7, 8 ps of sim...Figure 3.21 Interaction forces between the pair of atoms.Figure 3.22 Homogenous deformation of the atomic lattice.Figure 3.23 Initial (
Читать дальше

 and
and 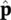 for various integration s...
for various integration s...










