Tadeusz Burczynski - Multiscale Modelling and Optimisation of Materials and Structures

The strength of coupling has some significant consequences. The strongly coupled models are usually faster and have a better mathematical and theoretical background. Usually, such models are solved with a single numerical method. However, phenomena in all scales must be described with consistent mathematical formulations (usually partial differential equations), which is rather hard or even not possible for some phenomena characterized, e.g.by stochastic behaviour. Moreover, the strongly coupled submodels cannot be separated, and their parts cannot be replaced with other submodels, which make their adaptation difficult. The weakly coupled models are more flexible, from both mathematical and numerical points of view, which makes their development and adaptation much easier. The coupling strength is linked with a methodology of data transfer between the scales.

Various classifications of the multiscale modelling methods were proposed having in mind all the aforementioned features of these techniques. Since this book is dedicated to simulations of materials processing methods, the multiscale models are classified into two groups: upscaling and concurrent approaches. In the upscaling class of methods, constitutive models at higher scales are constructed from observations and models at lower, more elementary scales [2]. By a sophisticated interaction between experimental observations at different scales and numerical solutions of constitutive models at increasingly larger scales, physically based models and their parameters can be derived at the macroscale. In this approach, it is natural that the microscale problem has to be solved at several locations in the macro‐model. For example, in the application of the concept of computational homogenization for each integration point of finite elements in the macroscale, the representative volume element (RVE) is considered in the microscale ( Figure 1.2).

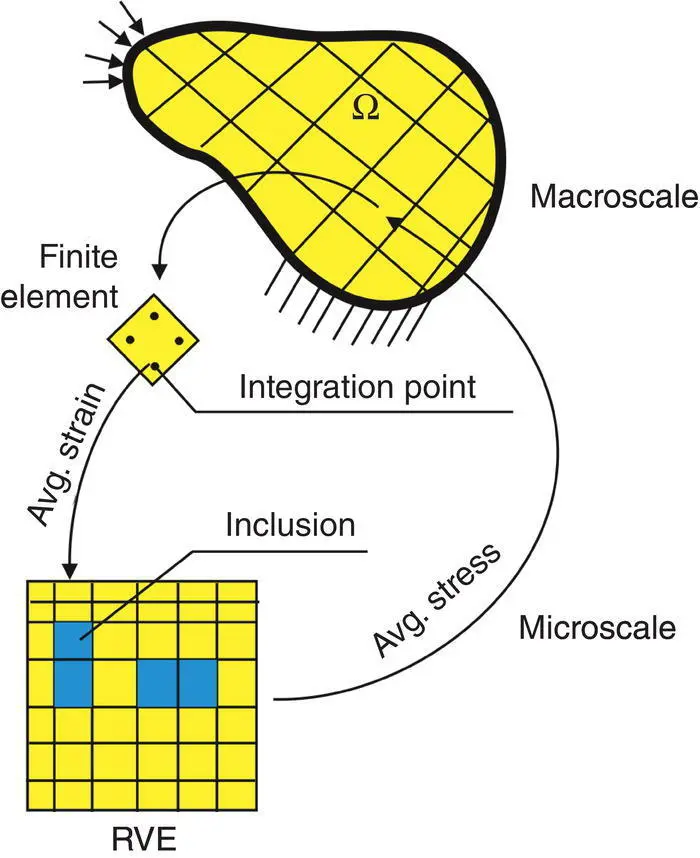
Figure 1.2 Illustration of computational homogenization concept.

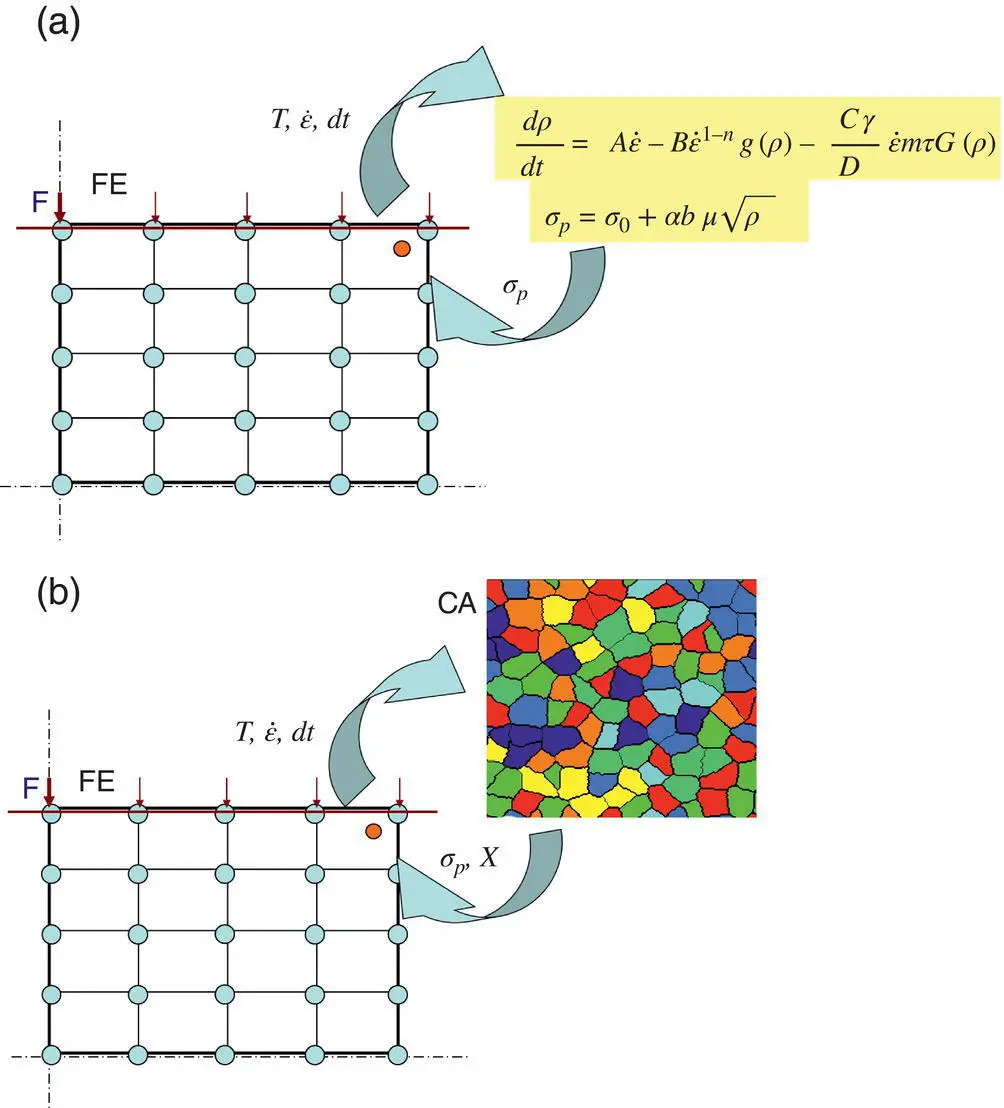
Figure 1.3 (a) Internal variable method as a precursor of upscaling and (b) the idea of the CAFE model.

Thus, classification of the multiscale problems with respect to the upscaling goals and the upscaling costs is needed, which is one of the book's objectives. The idea of upscaling has, in an intuitive manner, been used in engineering for decades. A commonly used approach based on a calculation of the flow stress in the FE model by a solution of the differential equation for the evolution of dislocation populations ( Figure 1.3a) can be considered the precursor of upscaling.

Significant progress was made when more advanced discrete methods were used in the microscale; see Figure 1.3b, where the CAFE method (cellular automata finite element) is shown as an example. Now we witness further development of multiscale methods in computational science, which couple fine and coarse scales more systematically. A variety of models and methods is used in both microscale/nanoscale and macroscale. The models are generally different for the two scales, but solutions using the same model in the coarse and fine scales are common. FE 2method is a typical example of such an approach [3].

In concurrent multiscale computing, one strives to solve the problem simultaneously at several scales (in practice two‐scales) by an a priori decomposition of the computational domain. Large‐scale problems are solved, and local data (e.g., displacements) are used as boundary conditions for a more detailed part of the problem. The question of how the fine scale is coupled to the coarse scale is essential in this approach. The major difficulty in coupling occurs when different models describe fine scales and coarse scales, for example coupling FE to MD. In other words, the objective is to find a computationally inexpensive but still accurate approach to the decomposition problem. The terms ‘homogenization’ and ‘localization’ are commonly used for operations during data transfer. Again, this terminology is not well defined. Homogenization, in multiscale modelling, has two meanings. In the context of strongly coupled models, based on differential equations, it is understood as the asymptotic homogenization, the method of studying partial differential equations with rapidly oscillating coefficients. The in‐depth description of the homogenization and the averaging based on the perturbation theory, as well as their application to multiscale modelling, can be found e.g.in [12]. However, most authors use this term differently, describing it as ‘any method of transforming a heterogeneous field into a homogeneous one’. Weighted averaging is usually used; however, more advanced techniques are also present. In this book, we use the term homogenization in common understanding and asymptotic homogenization in the sense of the element of perturbation theory. Details on the multiscale classification and examples of its applications can be found in Chapter 5of the book.

In recent years, a gradual paradigm shift has been taking place in the selection of materials to suit particular engineering requirements, especially in high‐performance applications. The empirical approach adopted by materials scientists and engineers in choosing materials parameters from a database is being replaced by design based on the DMR concept. Features that span across a large spectrum of length scales are altered and controlled to achieve the desired properties and performance at the macroscale. Research efforts, in this aspect, include the development of engineering materials by changing the composition, morphology, and topology of their constituents at the microscopic/mesoscopic level. The objective of this book is to show multiscale methods and their applications in computational materials design. From one side, we present computational multiscale material modelling based on the bottom‐up/top‐down, one‐way coupled description of the material structure in different representative scales. On the other side, our intention is to show possibilities of a combination of multiscale methods with optimization techniques.

Solution of optimization problems in multiscale modelling allows finding structures with better performance or strength in one scale with respect to design variables in another scale. In this case, the typical situation is to find a vector of material or geometrical parameters on the micro‐level, which minimizes an objective function dependent on state fields on a macro‐level of the structure.

A special case of optimization problems associated with the multiscale approach is the optimization of atomic clusters for the minimization of the system's potential energy. This case has an important consequence, especially in the design of new 2D nanomaterials and nanostructures.

The identification problem is formulated as the evaluation of some geometrical or material parameters of structures in one scale having measured information in another scale. The important case of identification in multiscale modelling is to find material properties, the shape of the inclusions/fibres or voids in the microstructure having measurements of state fields made on the macro‐object. The identification problem is formulated and considered as a special optimization task.

The analysis methods of multiscale models based on computational homogenization are adopted for these classes of problems. To solve optimization and identification problems, global optimization methods based on bioinspired algorithms are used.