Tadeusz Burczynski - Multiscale Modelling and Optimisation of Materials and Structures

This book's main feature, which distinguishes it from other publications, is that it is focused on modelling of processing of materials and that it combines the problem of multiscale modelling with the optimization tasks providing a wide range of possibilities for practical industrial applications.

The first part of the book contains a presentation of basic principles of the microscale and nanoscale modelling techniques. The second part supplies information about applications of optimization and identification techniques in multiscale modelling. The book is recapitulated by presenting information on the computer science techniques used in multiscale modelling, and it is focused on computer implementation issues, advising scientists interested in developing their multiscale models.

During the last years, numerical modelling became a widely used tool that successfully supports and comprehends experimental research on various modern materials. Basic principles of this modelling technique, as well as the classification of models, can be found in fundamental works of Allix [1] or Fish [4], and Horstemeyer and Wang [5] which discussed possible scopes of applications of multiscale modelling in the industry. However, within the last several years, various papers on multiscale modelling have been published in the scientific literature concerning both theoretical issues and practical applications. A variety of problems was raised in these papers, and several ambiguities connected with nomenclature and definitions can be found. The problem of naming various scales in multiscale modelling is an example of a lack of consistency in definitions. Commonly, ‘macro’, ‘meso’, ‘micro’, and ‘nano’ scales are mentioned ( Figure 1.1).

Nevertheless, this nomenclature can be misleading and often not sufficient. The term ‘macroscale’ is used for different scales, from large structures to single crystals. Others describe the single‐crystal level as ‘microscale’. In many cases, the characteristic entities in the particular scale are important, not the characteristic length. For example the characteristic length of the scale, in which grains are distinguishable, can vary from nanometres to centimetres. Moreover, the same grain‐level scale can be applied as macroscale in connection with an atomistic scale model or as microscale with a macroscopic model of a large structure deformation. Therefore, this book uses the term ‘coarse’ scale for the scale with greater characteristic length and ‘fine’ scale for the scale with smaller characteristic length. It allows using the terms ‘coarser’ and ‘finer’ to describe relations between more than two scales. To keep the concept clear, the fine or coarse scales are usually related to the governing structures in particular cases (e.g. grains, atoms). Despite the length scale problem, there is also an issue with the time scale as many of the phenomena occur in significantly different time regimes. Usually, the temporal scale is unified across the different length scales to provide physically relevant results, which sometimes makes the computational model expensive.

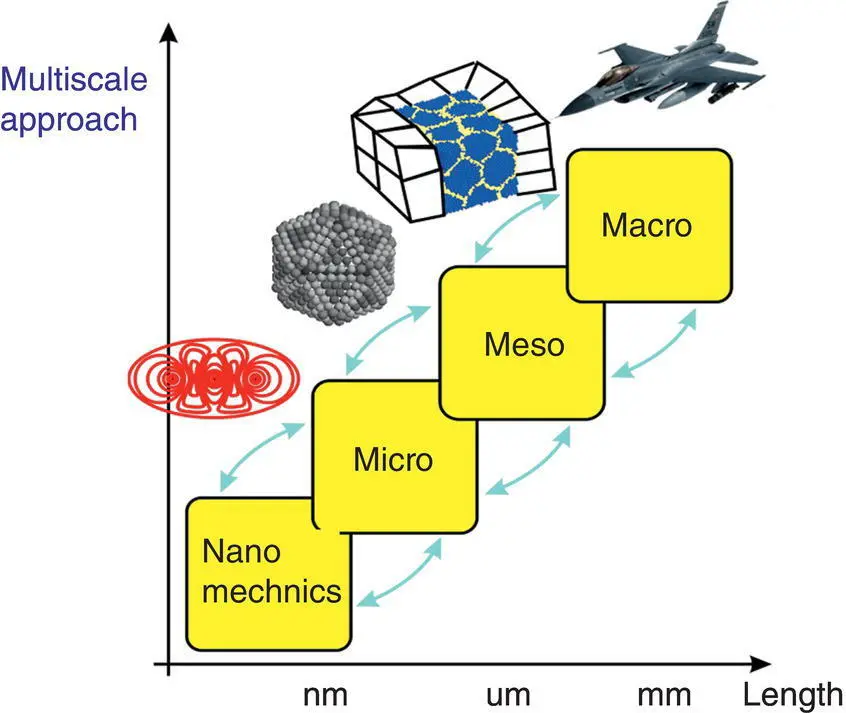
Figure 1.1 Multiscale concept diagram which illustrates ‘macro’, ‘meso’, ‘micro’, and ‘nano’ scales.

The lack of a definition for the term multiscale in the numerical modelling community is another problem. The broad understanding of multiscale modelling includes all problems with important features in multiple scales (temporal and spatial) [15]. Stricter definitions are also used. In the narrow sense of the term, modelling is multiscale when the models at different scales are simultaneously considered [13]. There is a fundamental difference between these two definitions. Important features at more than one scale are present in almost all problems of material science. A microstructural base of work hardening is one of the most common examples. Hardening is a process at a clearly different scale than plastic deformation modelled with a continuity assumption. Hence we can describe the simulation of plastic deformation and work hardening as the multiscale model. One can also define the multiscale model as a system of submodels at two or more scales but not necessarily simultaneously computed. Some examples are discussed in the book. Two submodels must work simultaneously when both are dependent on results from the second one. Such models are two‐way coupled, contrary to one‐way coupling where one of the models is independent.

The range of possible applications of multiscale modelling is extensive. It includes such different topics as social issues, economy, ecosystems, weather forecast, and physical and chemical processes occurring in gases, fluids, and solids. Material models are an essential branch of multiscale modelling, combining physical and chemical processes, mainly in solids. Such a wide variety of topics makes revising all multiscale modelling applications impossible. Even in material science, several families of applications can be distinguished. The main areas are modelling of polymers, composites, solidification, thin layers, or polycrystalline materials. Each of these areas has its own characteristic features, distinguishing them from the others. While the bases are common for all areas, possible solutions to particular problems are different.

In this book, applications of multiscale modelling to processes occurring in polycrystalline materials, mainly metals and their alloys, are reviewed and addressed. The most distinguishing feature of metals and their alloys is their unrepeatable microstructure. However, the atomistic structure of crystals is regular, while properties of these materials depend mostly on imperfections of atomic structures (dislocations, solid solutions of atoms, grain boundaries, etc.). The mesoscale picture of the material structures includes disordered (usually) distribution of grain shapes, sizes and orientations, as well as strong anisotropy of single crystals and grain boundaries. It is a significant difference in comparison with composites and polymers (with its repeatable microstructure). Then, the difference between the modelling of crystallization and thin layers deposition lies within lack or a very small amount of fluids. It must be remembered that modelling of fluids flow is governed by different types of equations. Moreover, numerical techniques for microscale models and coupling of scales are different in the presence of fluids. Due to this diversity in materials and different techniques used for their description, the book focuses mostly on mentioned metals and their alloys to provide in‐depth information on the practical application of dedicated multiscale modelling and optimization techniques.

As mentioned, in the field of metallic materials, several classifications of multiscale models exist. They depend on such issues as the character of coupling between the scales or methodology of data transformation between the scales. Coupling between the scales can be either strong or weak. Strong coupling combines a description of both (or more) scales into one equations system. In weak coupling, only some data are transferred between the subsequent scales. In the fine scale, the boundary or initial conditions can be developed based on coarse scale data (top‐down approach/downscaling), while data from the fine scale can be used as material properties or a material state in the coarse scale (bottom‐up approach/upscaling). Weakly coupled models have a relatively flexible structure and can be classified into top‐down and bottom‐up approaches.