Michael H. Veatch - Linear and Convex Optimization

In Section 1.2we introduced the concept of a linear program. This section introduces algebraic and matrix notation for linear programs. It then defines the three main classes of mathematical programs: linear programs, integer programs, and nonlinear programs. Each of these will be studied in later chapters, though for nonlinear programs we will focus on the more tractable subclass of convex programs. A mathematical program with variables and objective function 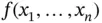can be stated abstractly in terms of a feasible region 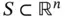as

However, we will always describe the feasible region using constraint equations or inequalities. The notation for the constraints is introduced in the following text.

We have already seen two examples of linear programs.

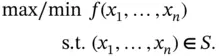
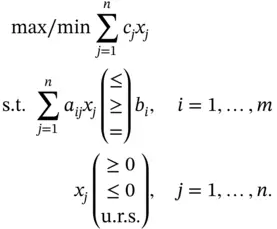
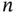There are decision variables, and 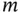functional constraints. The constraints can use a mixture of “ 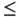”, “ ”, 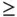and “ 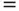”. Each variable may have the bound 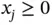, , 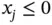or no bound, which we call unrestricted in sign (u.r.s.). The distinguishing characteristics of a linear program are (i) the objective function and all constraints are linear functions and (ii) the variables are continuous, i.e. fractional values are allowed. They are often useful as approximate models even when these assumptions do not fully hold.

We will use matrix notation for linear programs whenever possible. Let , , , and

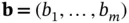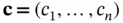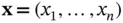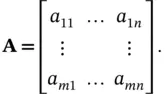
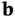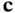Here , , and 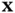are column vectors. If all the constraints are equalities, they can be written 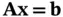. Similarly, “ 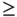” constraints can be written .

Example 1.2Consider the linear program

(1.4)

Converting the objective function and constraints to matrix form, we have

If we let

then this linear program can be written

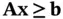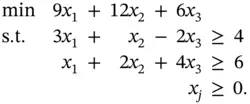
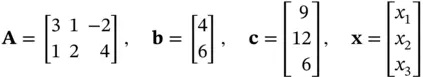
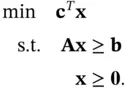
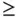It is important to distinguish between the structure of an optimization problem and the data that provides a specific numerical example. The structure of ( 1.4) is a minimization linear program with “ ” constraints and nonnegative variables; the data are the values in 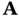, , 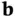and .

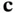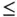To write a mixture of “ ” and “ 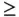” constraints, it is convenient to use submatrices

and write, e.g.

Many practical optimization problems involve making discrete quantitative choices, such as how many fire trucks of each type a fire department should purchase, or logical choices, such as whether or not each drug being developed by a pharmaceutical company should be chosen for a clinical trial. Both types of situations can be modeled by integer variables.