Consider again the linear program ( 1.1) with the alternative objective function ( 1.2). The variables represent the number of pallets of tents and food. If we restrict the variables to be integers, i.e. we can only load whole pallets, then the problem becomes an integer program and can be stated
(1.5) 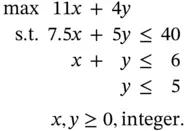
Without the integer restriction, it is a linear program with optimal solution  and optimal value
and optimal value  . However, because this solution is not integer (i.e. not all of its variables have integer values), it is not feasible for the integer program. Only solutions that have integer values and satisfy the constraints are feasible, as shown in Figure 1.4. Once we have determined the feasible points, an optimal solution can be found graphically by sweeping the contour line
. However, because this solution is not integer (i.e. not all of its variables have integer values), it is not feasible for the integer program. Only solutions that have integer values and satisfy the constraints are feasible, as shown in Figure 1.4. Once we have determined the feasible points, an optimal solution can be found graphically by sweeping the contour line  in the improving direction (upward). The last point touched by the line is optimal. In this case the last point is
in the improving direction (upward). The last point touched by the line is optimal. In this case the last point is 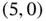 and the optimal value is
and the optimal value is  .
.

Figure 1.4Feasible integer solutions for ( 1.5).
Although the graphical method was fairly simple for this example, it is quite different than when solving linear programs. Note that:
There is not necessarily an optimal solution at the intersection of two constraints. In our example, lies only on the constraint line . In other examples, the optimal solution may not lie on any constraint.
The optimal solution is not necessarily obtained by rounding the linear program optimal solution. In fact, there is no limit to how far the optimal solution could be from the linear programming solution.
The integer program can be infeasible when the linear program is feasible.
These difficulties suggest that integer programs are harder to solve than linear programs, which we will see is true. Even solving a two‐variable integer program graphically can be tedious. However, we do not necessarily need to generate all integer feasible solutions. For example, if we start by generating the feasible point 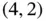 , then we draw the contour line through it and check for integer points in the linear program's feasible region and above the contour. Checking points to the right of
, then we draw the contour line through it and check for integer points in the linear program's feasible region and above the contour. Checking points to the right of  (because this contour does not touch the feasible region for
(because this contour does not touch the feasible region for  ),
),  is infeasible but
is infeasible but  qualifies, so it is optimal. The idea of using a feasible integer solution to eliminate other integer points from consideration will be used in Chapter 13.
qualifies, so it is optimal. The idea of using a feasible integer solution to eliminate other integer points from consideration will be used in Chapter 13.
The general form of an integer program is the same as a linear program with the added constraint that the variables are integers. If only some of the variables are restricted to be integer, it is called a mixed integer program . When variables represent logical choices, they are usually defined so that  if true (decide to take the action) and
if true (decide to take the action) and  if false (decide not to take the action). A variable whose possible values are
if false (decide not to take the action). A variable whose possible values are  is called a binary variable . An integer program with all binary variables is called a binary program .
is called a binary variable . An integer program with all binary variables is called a binary program .
General Form of an Integer Program

An optimization problem where the objective function and constraints may be nonlinear is called a nonlinear program . The variables are assumed to be continuous, as in a linear program. Thus, nonlinear programs are more general than linear programs, but do not include integer programs. While linear programs can be described in matrix notation, nonlinear programs are described in terms of functions.
General Form of a Nonlinear Program

We have not stated the nonnegativity constraints separately. However, a nonnegativity constraint can be included in the functional constraints if needed.
The ability to solve a nonlinear program depends on the type of objective function  and constraints
and constraints  . A class of more easily solved nonlinear programs called convex programs is discussed in Chapters 14and 15. Also, Chapter 3shows how certain piece‐wise linear convex programs can be converted into linear programs, which is useful because convex programs are somewhat harder to solve than linear programs.
. A class of more easily solved nonlinear programs called convex programs is discussed in Chapters 14and 15. Also, Chapter 3shows how certain piece‐wise linear convex programs can be converted into linear programs, which is useful because convex programs are somewhat harder to solve than linear programs.
For Exercises 1–6, solve the linear program graphically.
For Exercises 6–8, solve the integer program graphically.
1
2
3
4 a) Solve as stated. b) Change “min” to “max” and solve.
5
6
7
8
9 For the linear program (1.1)Suppose the objective is to minimize the cost of aid given in 1.2. What is the optimal solution? Explain why minimizing cost is not a reasonable objective for this problem.Find an objective function for which , is optimal. Show graphically that this point is optimal.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Читать дальше

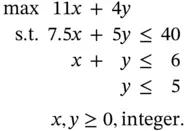
 and optimal value
and optimal value  . However, because this solution is not integer (i.e. not all of its variables have integer values), it is not feasible for the integer program. Only solutions that have integer values and satisfy the constraints are feasible, as shown in Figure 1.4. Once we have determined the feasible points, an optimal solution can be found graphically by sweeping the contour line
. However, because this solution is not integer (i.e. not all of its variables have integer values), it is not feasible for the integer program. Only solutions that have integer values and satisfy the constraints are feasible, as shown in Figure 1.4. Once we have determined the feasible points, an optimal solution can be found graphically by sweeping the contour line  in the improving direction (upward). The last point touched by the line is optimal. In this case the last point is
in the improving direction (upward). The last point touched by the line is optimal. In this case the last point is 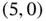 and the optimal value is
and the optimal value is  .
.
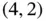 , then we draw the contour line through it and check for integer points in the linear program's feasible region and above the contour. Checking points to the right of
, then we draw the contour line through it and check for integer points in the linear program's feasible region and above the contour. Checking points to the right of  (because this contour does not touch the feasible region for
(because this contour does not touch the feasible region for  ),
),  is infeasible but
is infeasible but  qualifies, so it is optimal. The idea of using a feasible integer solution to eliminate other integer points from consideration will be used in Chapter 13.
qualifies, so it is optimal. The idea of using a feasible integer solution to eliminate other integer points from consideration will be used in Chapter 13. if true (decide to take the action) and
if true (decide to take the action) and  if false (decide not to take the action). A variable whose possible values are
if false (decide not to take the action). A variable whose possible values are  is called a binary variable . An integer program with all binary variables is called a binary program .
is called a binary variable . An integer program with all binary variables is called a binary program .

 and constraints
and constraints  . A class of more easily solved nonlinear programs called convex programs is discussed in Chapters 14and 15. Also, Chapter 3shows how certain piece‐wise linear convex programs can be converted into linear programs, which is useful because convex programs are somewhat harder to solve than linear programs.
. A class of more easily solved nonlinear programs called convex programs is discussed in Chapters 14and 15. Also, Chapter 3shows how certain piece‐wise linear convex programs can be converted into linear programs, which is useful because convex programs are somewhat harder to solve than linear programs.










