1 Graph the region that satisfies all of the constraints.
2 Draw a contour line of the objective function and determine which direction improves the objective function. A second contour line can be used to determine which direction is improving.
3 Sweep the contour line in the improving direction, generating parallel lines, until it is about to leave the region. The last line intersecting the region has the optimal objective function value. The point(s) where this line intersects the region is optimal.
4 Find the coordinates of an optimal point by solving a system of two linear equations from the constraints whose lines pass through this point.
If the set of points satisfying the constraints is nonempty and bounded, then an optimal solution exists and the method earlier will find it. The other cases are discussed in Section 1.3.
Viewing the problem graphically brings up several questions about linear programs that will be answered in later chapters. First, the optimal value occurred at a corner point of the region, where two (or more) constraint lines intersect. Will this always be the case? Second, the idea of sweeping the contour line until it leaves the region assumes that contour lines 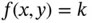 intersect points satisfying the constraints for
intersect points satisfying the constraints for 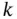 in a single interval. Thus, an optimal objective function value is one where lines with slightly larger
in a single interval. Thus, an optimal objective function value is one where lines with slightly larger 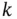 do not touch the region. Is it possible for the contour line to leave the region and reenter it? That is, for
do not touch the region. Is it possible for the contour line to leave the region and reenter it? That is, for 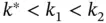 if the line for
if the line for 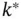 touches the region and the line for
touches the region and the line for 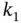 does not, it possible for the line for
does not, it possible for the line for 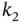 to touch the region? If so, we would have to do more checking to find the optimal
to touch the region? If so, we would have to do more checking to find the optimal 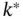 . Related to this is the question of local maxima. The point
. Related to this is the question of local maxima. The point 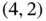 is called a local maximum as it has the largest objective function value of all points in a small circle around
is called a local maximum as it has the largest objective function value of all points in a small circle around 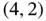 . It is easier to check that it is a local maximum than examining all points that satisfy the constraints to check that it is a global maximum. Is it always true that a local maximum is also a global maximum? Finally, the region in Figure 1.2is defined by the constraints, but the optimal point depends on the objective function. For example, if instead we wish to maximize
. It is easier to check that it is a local maximum than examining all points that satisfy the constraints to check that it is a global maximum. Is it always true that a local maximum is also a global maximum? Finally, the region in Figure 1.2is defined by the constraints, but the optimal point depends on the objective function. For example, if instead we wish to maximize
(1.2) 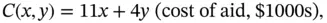
the optimal load is 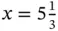 pallets of tents and
pallets of tents and 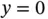 pallets of food, with a cost of $58 667. However, for small changes in the coefficients of
pallets of food, with a cost of $58 667. However, for small changes in the coefficients of 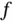 , the point
, the point 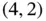 is still optimal. How much can an objective function coefficient be changed without changing the optimal point?
is still optimal. How much can an objective function coefficient be changed without changing the optimal point?
The fractional solution 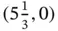 makes sense in this problem: one pallet is re‐packed with
makes sense in this problem: one pallet is re‐packed with 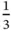 as much food. In other problems, fractional solutions may not make sense. They can either be interpreted as approximate solutions that must be converted to integers to be implemented, or a different optimization problem can be studied, where the variables are discrete, only taking on integer values.
as much food. In other problems, fractional solutions may not make sense. They can either be interpreted as approximate solutions that must be converted to integers to be implemented, or a different optimization problem can be studied, where the variables are discrete, only taking on integer values.
1.2.1 The Modeling Process
As we move from this small linear program to more general and complex models, some guidelines on modeling will be helpful. When formulating a mathematical program, it is not always obvious what the decision variables should be. There are often multiple approaches to defining the variables and there can be pros and cons to different approaches. The objective is intended to reflect the priorities of the decision‐maker. To pose the situation as a mathematical program, an objective must be chosen. This may be very clear, as when maximizing profit, or much more subtle, as in the example previously. The constraints may include physical, logical, financial, or other limitations. They may also reflect policies that the decision‐maker applies. Finally, a constraint may simply be an equation that defines an auxiliary variable that is used to write the problem more concisely.
Another theme that will emerge is the difference between specific and general models. We will often use algebraic notation for (some of) the constants in a model, rather than numbers. This allows us to separate the data that goes into a model from its structure. It is this structure that defines the general model. There are multiple levels of generality to a model used in an application. One way to generalize is to allow any size of the problem: instead of two items being loaded, there could be 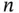 items. To make a model more specific, we often add constraints with a special structure to describe a specific situation.
items. To make a model more specific, we often add constraints with a special structure to describe a specific situation.
The examples in this book take a verbal description of an optimization problem and translate it into mathematics. There is much more involved in using models to guide decisions. The overall modeling process may involve:
1 Problem definition. The first step is to identify the problem that the decision‐maker faces. This includes specifying the objective and the system to be studied.
2 Data collection. The next step is to collect data that is relevant to the model. This may entail observing the system or obtaining data that is already recorded.
3 Model formulation. In this step the analyst formulates a mathematical model of the decision problem. It involves translation into mathematical language, but also abstraction or simplification of a complex operation into a manageable problem.
4 Model solution. For optimization problems, this step finds an optimal or near‐optimal solution. Generally this is done numerically using an algorithm, rather than algebraically.
Читать дальше

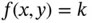 intersect points satisfying the constraints for
intersect points satisfying the constraints for 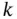 in a single interval. Thus, an optimal objective function value is one where lines with slightly larger
in a single interval. Thus, an optimal objective function value is one where lines with slightly larger 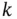 do not touch the region. Is it possible for the contour line to leave the region and reenter it? That is, for
do not touch the region. Is it possible for the contour line to leave the region and reenter it? That is, for 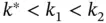 if the line for
if the line for 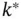 touches the region and the line for
touches the region and the line for 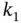 does not, it possible for the line for
does not, it possible for the line for 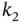 to touch the region? If so, we would have to do more checking to find the optimal
to touch the region? If so, we would have to do more checking to find the optimal 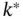 . Related to this is the question of local maxima. The point
. Related to this is the question of local maxima. The point 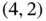 is called a local maximum as it has the largest objective function value of all points in a small circle around
is called a local maximum as it has the largest objective function value of all points in a small circle around 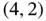 . It is easier to check that it is a local maximum than examining all points that satisfy the constraints to check that it is a global maximum. Is it always true that a local maximum is also a global maximum? Finally, the region in Figure 1.2is defined by the constraints, but the optimal point depends on the objective function. For example, if instead we wish to maximize
. It is easier to check that it is a local maximum than examining all points that satisfy the constraints to check that it is a global maximum. Is it always true that a local maximum is also a global maximum? Finally, the region in Figure 1.2is defined by the constraints, but the optimal point depends on the objective function. For example, if instead we wish to maximize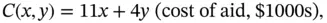
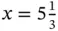 pallets of tents and
pallets of tents and 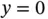 pallets of food, with a cost of $58 667. However, for small changes in the coefficients of
pallets of food, with a cost of $58 667. However, for small changes in the coefficients of 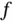 , the point
, the point 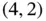 is still optimal. How much can an objective function coefficient be changed without changing the optimal point?
is still optimal. How much can an objective function coefficient be changed without changing the optimal point?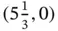 makes sense in this problem: one pallet is re‐packed with
makes sense in this problem: one pallet is re‐packed with 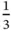 as much food. In other problems, fractional solutions may not make sense. They can either be interpreted as approximate solutions that must be converted to integers to be implemented, or a different optimization problem can be studied, where the variables are discrete, only taking on integer values.
as much food. In other problems, fractional solutions may not make sense. They can either be interpreted as approximate solutions that must be converted to integers to be implemented, or a different optimization problem can be studied, where the variables are discrete, only taking on integer values.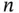 items. To make a model more specific, we often add constraints with a special structure to describe a specific situation.
items. To make a model more specific, we often add constraints with a special structure to describe a specific situation.










