1 Cover
2 Title Page Linear Algebra Michael L. O’Leary
3 Copyright
4 Dedication
5 Preface
6 Acknowledgments
7 About the Companion Website
8 CHAPTER 1: Logic and Set Theory1.1 Statements 1.2 Sets and Quantification 1.3 Sets and Proofs 1.4 Functions
9 CHAPTER 2: Euclidean Space 2.1 Vectors 2.2 Dot Product 2.3 Cross Product
10 CHAPTER 3: Transformations and Matrices3.1 Linear Transformations 3.2 Matrix Algebra 3.3 Linear Operators 3.4 Injections and Surjections 3.5 Gauss‐Jordan Elimination
11 CHAPTER 4: Invertibility4.1 Invertible Matrices 4.2 Determinants 4.3 Inverses and Determinants 4.4 Applications
12 CHAPTER 5: Abstract Vectors 5.1 Vector Spaces 5.2 Subspaces 5.3 Linear Independence 5.4 Basis and Dimension 5.5 Rank and Nullity 5.6 Isomorphism
13 CHAPTER 6: Inner Product Spaces6.1 Inner Products 6.2 Orthonormal Bases
14 CHAPTER 7: Matrix Theory7.1 Eigenvectors and Eigenvalues 7.2 Minimal Polynomial 7.3 Similar Matrices 7.4 Diagonalization
15 Further Reading
16 Index
17 End User License Agreement
1 Chapter 1 Figure 1.1 A function f ⊆ A × B . Figure 1.2 The composition of f and g . Figure 1.3 g is not a one‐to‐one function. Figure 1.4 h is a one‐to‐one function. Figure 1.5 f is an onto function. Figure 1.6 g is a bijection. Figure 1.7 The image of C under f . Figure 1.8 The inverse image of D under f .
2 Chapter 2Figure 2.1 Two interpretations of vector as an arrow.Figure 2.2 Addition of arrows.Figure 2.3 Scaling ofarrows.Figure 2.4 Finding the distance between vectors.Figure 2.5 A triangle in ℝ 3.Figure 2.6 The distance between u and v is ‖u − v‖...Figure 2.7 The line L containing u with direction vector m.Figure 2.8 The plane P containing u with direction vectors m and n.Figure 2.9 Lines L and L′ with normal n.Figure 2.10 u= r v+ wwith w orthogonal to v.Figure 2.11 The distance from the vector u to the plane P .Figure 2.12 The distance from the vector u to the plane P , side view.Figure 2.13 Computing the cross product.Figure 2.14 The parallelogram described by u and v.Figure 2.15 The parallelepiped described by u, v, and w.
3 Chapter 3Figure 3.1 Linear transformations preserve addition.Figure 3.2 Linear transformations preserve scalar multiplication.Figure 3.3 A reflection through the line ℓ .Figure 3.4 A reflection in ℝ 2through the line L .Figure 3.5 A reflection in ℝ 3through the xy ‐plane.Figure 3.6 A rotation of θ centered at O .Figure 3.7 A rotation in ℝ 2through θ .Figure 3.8 A rotation in ℝ 3about the z ‐axis through θ .Figure 3.9 A rotation in ℝ 3about the z ‐axis through θ viewed fro...Figure 3.10 A rotation in ℝ 3of e 3and e 1about the y ‐axis through θ ...Figure 3.11 A reflection is an isometry.Figure 3.12 A rotation is an isometry.Figure 3.13 A translation is anisometry.Figure 3.14 A shear along L .Figure 3.15 A horizontal shear with shear factor k .
4 Chapter 4Figure 4.1 The parallelogram described by uand v.Figure 4.2 The parallelogram described by T uand T v.Figure 4.3 The areas of a parallelogram and its image under a linear operato...
5 Chapter 5Figure 5.1 Illustrating the Rank‐Nullity Theorem.Figure 5.2 Writing w as a linear combination of two bases.Figure 5.3 Change of basis 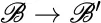 Figure 5.4 Diagram for the change of basis transformation
Figure 5.4 Diagram for the change of basis transformation 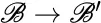 .Figure 5.5 Change of basis
.Figure 5.5 Change of basis 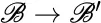 with linear transformation T .Figure 5.6 Diagram for the standard transformation
with linear transformation T .Figure 5.6 Diagram for the standard transformation 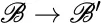 .
.
6 Chapter 6Figure 6.1 The projection of u 2onto v 1.Figure 6.2 Finding a vector orthogonal to S( v 1, v 2). Figure 6.3 The projection of u 3onto v 1.
7 Chapter 7Figure 7.1 The ellipse 7 x 2+ 4 xy + 4 y 2= 16 wi...
1 Cover
2 Table of Contents
3 Begin Reading
1 iii
2 iv
3 v
4 xi
5 xii
6 xiii
7 xiv
8 xv
9 xvi
10 1
11 2
12 3
13 4
14 5
15 6
16 7
17 8
18 9
19 10
20 11
21 12
22 13
23 14
24 15
25 16
26 17
27 18
28 19
29 20
30 21
31 22
32 23
33 24
34 25
35 26
36 27
37 28
38 29
39 30
40 31
41 32
42 33
43 34
44 35
45 36
46 37
47 38
48 39
49 40
50 41
51 42
52 43
53 44
54 45
55 46
56 47
57 49
58 50
59 51
60 52
61 53
62 54
63 55
64 56
65 57
66 58
67 59
68 60
69 61
70 62
71 63
72 64
73 65
74 66
75 67
76 68
77 69
78 70
79 71
80 72
81 73
82 74
83 75
84 76
85 77
86 78
87 79
88 80
89 81
90 82
91 83
92 84
93 85
94 86
95 87
96 88
97 89
98 90
99 91
100 92
101 93
102 94
103 95
104 96
105 97
106 99
107 100
108 101
109 102
110 103
111 104
112 105
113 106
114 107
115 108
116 109
117 110
118 111
119 112
120 113
121 114
122 115
123 116
124 117
125 118
126 119
127 120
128 121
129 122
130 123
131 124
132 125
133 126
134 127
135 128
136 129
137 130
138 131
139 132
140 133
141 134
142 135
143 136
144 137
145 138
146 139
147 140
148 141
149 142
150 143
151 144
152 145
153 146
154 147
155 148
156 149
157 150
158 151
159 152
160 153
161 154
162 155
163 156
164 157
165 158
166 159
167 160
168 161
169 162
170 163
171 164
172 165
173 166
174 167
175 168
176 169
177 170
178 171
179 172
180 173
181 174
182 175
183 176
184 177
185 178
186 179
187 180
188 181
189 182
190 183
191 184
192 185
193 186
194 187
195 188
196 189
197 190
198 191
199 192
200 193
201 194
202 195
203 196
204 197
205 198
206 199
207 200
208 201
209 202
210 203
211 204
212 205
213 206
Читать дальше

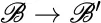 Figure 5.4 Diagram for the change of basis transformation
Figure 5.4 Diagram for the change of basis transformation 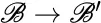 .Figure 5.5 Change of basis
.Figure 5.5 Change of basis 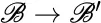 with linear transformation T .Figure 5.6 Diagram for the standard transformation
with linear transformation T .Figure 5.6 Diagram for the standard transformation 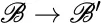 .
.










