
1 Cover
2 Linear and Convex Optimization Linear and Convex Optimization A Mathematical Approach Michael H. Veatch Gordon College
3 Copyright
4 Preface
5 About the Companion Website
6 1 Introduction to Optimization Modeling1.1 Who Uses Optimization? 1.2 Sending Aid to a Disaster 1.3 Optimization Terminology 1.4 Classes of Mathematical Programs
7 2 Linear Programming Models 2.1 Resource Allocation 2.2 Purchasing and Blending 2.3 Workforce Scheduling 2.4 Multiperiod Problems 2.5 Modeling Constraints 2.6 Network Flow
8 3 Linear Programming Formulations 3.1 Changing Form 3.2 Linearization of Piecewise Linear Functions 3.3 Dynamic Programming
9 4 Integer Programming Models 4.1 Quantitative Variables and Fixed Costs 4.2 Set Covering 4.3 Logical Constraints and Piecewise Linear Functions 4.4 Additional Applications 4.5 Traveling Salesperson and Cutting Stock Problems
10 5 Iterative Search Algorithms 5.1 Iterative Search and Constructive Algorithms 5.2 Improving Directions and Optimality 5.3 Computational Complexity and Correctness
11 6 Convexity 6.1 Convex Sets 6.2 Convex and Concave Functions
12 7 Geometry and Algebra of LPs 7.1 Extreme Points and Basic Feasible Solutions 7.2 Optimality of Extreme Points 7.3 Linear Programs in Canonical Form 7.4 Optimality Conditions 7.5 Optimality for General Polyhedra
13 8 Duality Theory 8.1 Dual of a Linear Program 8.2 Duality Theorems 8.3 Complementary Slackness 8.4 Lagrangian Duality 8.5 Farkas' Lemma and Optimality
14 9 Simplex Method 9.1 Simplex Method From a Known Feasible Solution 9.2 Degeneracy and Correctness 9.3 Finding an Initial Feasible Solution 9.4 Computational Strategies and Speed
15 10 Sensitivity Analysis 10.1 Graphical Sensitivity Analysis 10.2 Shadow Prices and Reduced Costs 10.3 Economic Interpretation of the Dual
16 11 Algorithmic Applications of Duality 11.1 Dual Simplex Method 11.2 Network Simplex Method 11.3 Primal‐Dual Interior Point Method
17 12 Integer Programming Theory 12.1 Linear Programming Relaxations 12.2 Strong Formulations 12.3 Unimodular Matrices
18 13 Integer Programming Algorithms 13.1 Branch and Bound Methods 13.2 Cutting Plane Methods
19 14 Convex Programming: Optimality Conditions 14.1 KKT Optimality Conditions 14.2 Lagrangian Duality
20 15 Convex Programming: Algorithms 15.1 Convex Optimization Models 15.2 Separable Programs 15.3 Unconstrained Optimization 15.4 Quadratic Programming 15.5 Primal‐dual Interior Point Method
21 A Linear Algebra and Calculus ReviewA.1 Sets and Other Notation A.2 Matrix and Vector Notation A.3 Matrix Operations A.4 Matrix Inverses A.5 Systems of Linear Equations A.6 Linear Independence and Rank A.7 Quadratic Forms and Eigenvalues A.8 Derivatives and Convexity
22 Bibliography
23 Index
24 End User License Agreement
1 Chapter 1 Table 1.1 Data for sending aid.
2 Chapter 2 Table 2.1 Data for Kan Jam production. Table 2.2 Data for auto parts production. Table 2.3 Data for Custom Tees ads. Table 2.4 Data for producing steel. Table 2.5 Solution for producing steel. Table 2.6 Requirements and costs for police shifts. Table 2.7 Demand and labor available for gift baskets Table 2.8 Transmission costs, supply, and demand. Table 2.9 Soybean shipping costs, supply, and demand.
3 Chapter 4Table 4.1 Languages and costs for translators.Table 4.2 Processing times for interventions against an intruder.Table 4.3 Mileage between cities.
4 Chapter 7Table 7.1 Basic solutions for Example 7.6.
5 Chapter 8Table 8.1 Dual relationships.Table 8.2 Possibilities when solving the primal and the dual.Table 8.3 When Systems 1 and 2 have solutions.
6 Chapter 9Table 9.1 Reduced costs and simplex directions for Example 9.5.
7 Chapter 10Table 10.1 General terminology for a linear program.Table 10.2 Sign of shadow prices.Table 10.3 Data for Kan Jam production.Table 10.4 Data for Custom Tees ads.
8 Chapter 11Table 11.1 Dual relationships for corresponding basic solutions.Table 11.2 Iterations of the path following algorithm.Table 11.3 Points on central path.
1 Chapter 1 Figure 1.1 Region satisfying constraints for sending aid. Figure 1.2 Optimal point and contour for sending aid. Figure 1.3 Problem has optimal solution for dashed objective but is unbounde... Figure 1.4 Feasible integer solutions for (1.5).
2 Chapter 2 Figure 2.1 Electricity transmission network. Figure 2.2 Transportation network for soybeans.Figure 2.3 Water pipe network for Exercise 2.25.
3 Chapter 3Figure 3.1 Profit contribution (the negative of cost) for labor.Figure 3.2 Street grid. Each block is labeled with its travel time and each ...Figure 3.3 Travel times for Exercise 3.12.Figure 3.4 Project costs for Exercise 3.13.
4 Chapter 4Figure 4.1 A piecewise linear function.
5 Chapter 5Figure 5.1 An improving direction for maximizing 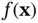 .
.
6 Chapter 6Figure 6.1 Feasible region and isocontours for Example 6.1.Figure 6.2 The first set is convex. The second is not.Figure 6.3 The point 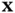 is a convex combination of
is a convex combination of 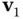 ,
, 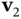 ,
, 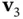 .Figure 6.4 Unbounded sets. Only the first two have unbounded directions.Figure 6.5 A polyhedral cone.Figure 6.6 The first function is convex. The second is concave.Figure 6.7 The line
.Figure 6.4 Unbounded sets. Only the first two have unbounded directions.Figure 6.5 A polyhedral cone.Figure 6.6 The first function is convex. The second is concave.Figure 6.7 The line 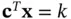 only intersects
only intersects 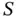 at the point shown.Figure 6.8 Epigraph of
at the point shown.Figure 6.8 Epigraph of 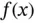 .
.
7 Chapter 7Figure 7.1 Basic solutions for Example 7.1.Figure 7.2 The point 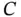 is a degenerate basic feasible solution.Figure 7.3 Feasible region for Example 7.3.Figure 7.4 Edge directions for the bfs
is a degenerate basic feasible solution.Figure 7.3 Feasible region for Example 7.3.Figure 7.4 Edge directions for the bfs 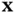 .Figure 7.5 Cones and their extreme rays
.Figure 7.5 Cones and their extreme rays 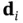 .
.
8 Chapter 8Figure 8.1 Gradient vectors and lines of constant 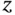 .Figure 8.2 Gradient vectors and active constraint normal vectors.
.Figure 8.2 Gradient vectors and active constraint normal vectors.
9 Chapter 9Figure 9.1 A polygon with 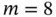 sides has diameter 4.
sides has diameter 4.
10 Chapter 10Figure 10.1 Feasible region for (10.1) with constraint 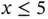 .Figure 10.2 Feasible region for 10.1 with
.Figure 10.2 Feasible region for 10.1 with 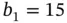 .Figure 10.3 Optimal value as a function of
.Figure 10.3 Optimal value as a function of 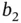 .Figure 10.4 Feasible regions with right‐hand sides
.Figure 10.4 Feasible regions with right‐hand sides 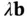 .
.
Читать дальше


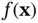 .
.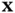 is a convex combination of
is a convex combination of 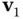 ,
, 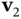 ,
, 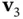 .Figure 6.4 Unbounded sets. Only the first two have unbounded directions.Figure 6.5 A polyhedral cone.Figure 6.6 The first function is convex. The second is concave.Figure 6.7 The line
.Figure 6.4 Unbounded sets. Only the first two have unbounded directions.Figure 6.5 A polyhedral cone.Figure 6.6 The first function is convex. The second is concave.Figure 6.7 The line 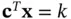 only intersects
only intersects 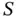 at the point shown.Figure 6.8 Epigraph of
at the point shown.Figure 6.8 Epigraph of 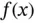 .
.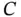 is a degenerate basic feasible solution.Figure 7.3 Feasible region for Example 7.3.Figure 7.4 Edge directions for the bfs
is a degenerate basic feasible solution.Figure 7.3 Feasible region for Example 7.3.Figure 7.4 Edge directions for the bfs 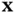 .Figure 7.5 Cones and their extreme rays
.Figure 7.5 Cones and their extreme rays 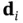 .
.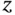 .Figure 8.2 Gradient vectors and active constraint normal vectors.
.Figure 8.2 Gradient vectors and active constraint normal vectors.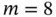 sides has diameter 4.
sides has diameter 4.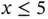 .Figure 10.2 Feasible region for 10.1 with
.Figure 10.2 Feasible region for 10.1 with 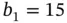 .Figure 10.3 Optimal value as a function of
.Figure 10.3 Optimal value as a function of 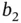 .Figure 10.4 Feasible regions with right‐hand sides
.Figure 10.4 Feasible regions with right‐hand sides 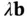 .
.










