Michael H. Veatch - Linear and Convex Optimization

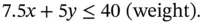
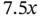In this expression, 7.5 is the weight per pallet of tents, so is the weight of tents. Similarly, 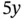is the weight of food. The left‐hand side, then, is the total weight of the load, which must be less than or equal to the payload capacity of 40 (these quantities are in 1000s of lbs). The space limit requires that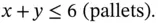

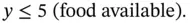
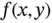The left‐hand side is the total number of pallets. This total does not have to be an integer; a total of 5.4 pallets would mean that one pallet is only loaded 40% full. Finally, only five pallets of food are ready, so

These inequalities define the domain of . We will call them constraints and the function 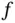to be maximized the objective function . Optimizing a function whose domain is defined by constraints is a constrained optimization problem. The complete problem is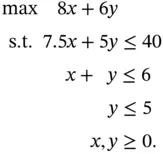

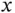(1.1)

We have abbreviated “subject to” as “s.t.”

Constrained optimization problems have three components:

1 1. The decision variables.

2 2. The objective function to be maximized or minimized, as a function of the decision variables.

3 3. The constraints that the decision variables are subject to.

The formulation of this problem consists of the Eqs. ( 1.1) and the definitions of the variables. It is essential to define the variables and also good practice to label or describe the objective function and each constraint. This problem is an example of a linear program because the variables are continuous and the objective function and all constraints are linear.

Now that we have formulated the loading decisions as a linear program, how do we solve it? For and 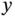to satisfy the constraints, they must lie in the intersection of the half planes defined by these inequalities, shown in Figure 1.1. Most linear inequalities can be conveniently graphed by finding the 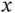and 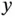intercept of the corresponding equation, drawing a line between them, and checking a point not on the line, such as 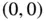, to see if it satisfies the inequality. If the point satisfies the inequality, then the half‐plane is on the same side of the line as that point; if the point does not satisfy the inequality, the half‐plane is on the other side of the line as that point. 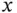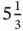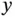For the first constraint (weight), the intercept is , the intercept is 8, and (0,0) is on the correct side of the line. Other constraints, such as 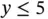, have horizontal or vertical boundary lines. Once all of the constraints have been graphed, we can identify the region (or possibly a line or a point) satisfying all the constraints. We are seeking the point in this region that has the largest value of 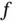. One way to find this point graphically is to plot contour lines 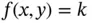for one or two values of 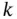. For example, in Figure 1.1the contours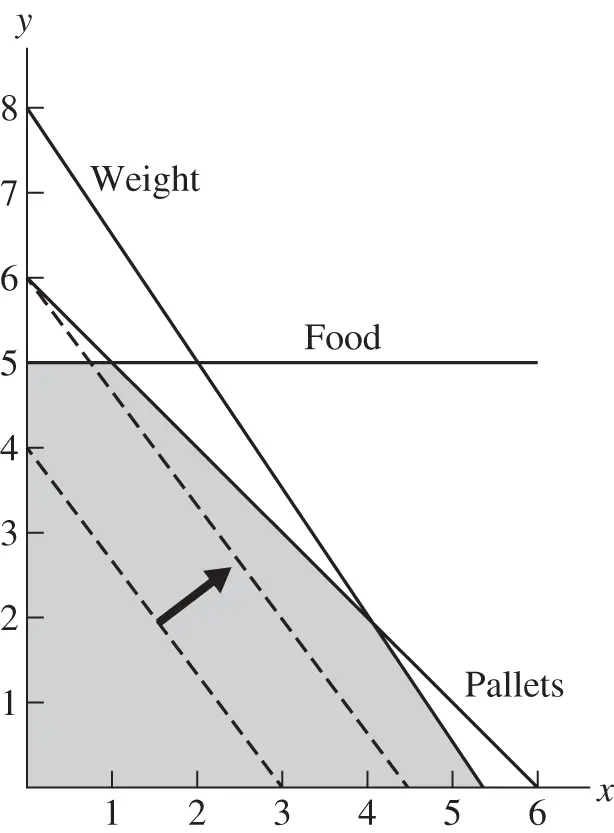

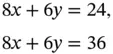
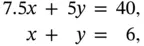
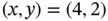Figure 1.1Region satisfying constraints for sending aid.

are graphed as dashed lines. They both intersect the shaded region, so there are points satisfying the constraints with objective function values of 24 and 36. Since all contour lines are parallel, we can visualize sweeping the line up and to the right without rotating it to find larger objective function values. The farthest contour line that touches the shaded region is shown in Figure 1.2. The point where it touches the region has the largest objective function value. This point lies on the constraint lines for weight and pallets, so we can find it by solving these two constraints with equality in place of inequality:

with solution and objective function value 44. This agrees with Figure 1.2, where the contour line drawn is 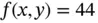. Thus, the optimal load is four pallets of tents and two pallets of food, with an expected value of 44.

Figure 1.2Optimal point and contour for sending aid.

To summarize, to solve a linear program with two variables graphically: