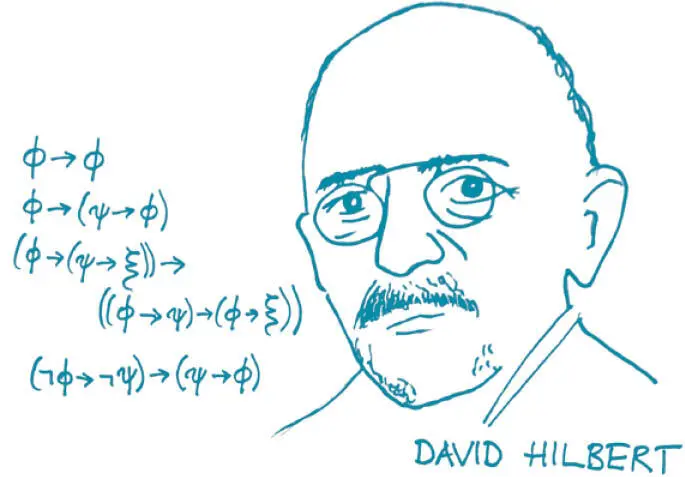Florian Aigner - Die Schwerkraft ist kein Bauchgefühl

Das erste Axiom legt eigentlich bloß einen Namen fest: „Null ist eine natürliche Zahl.“ Das zweite Axiom sagt bereits etwas Wichtiges über die Struktur der Zahlen aus: „Jede natürliche Zahl hat eine natürliche Zahl als Nachfolger.“ Auf diesen Nachfolger kann man dann natürlich gleich dieselbe Regel anwenden, auch diese Zahl muss wieder eine natürliche Zahl als Nachfolger haben. Das bedeutet, dass es eine Kette natürlicher Zahlen gibt, die keinen Endpunkt hat. Aber wie sieht diese Kette aus? Das dritte Axiom sagt: „Null ist nicht der Nachfolger einer natürlichen Zahl.“ Die Null spielt also eine Sonderrolle: Sie ist der Anfangspunkt der Kette.

Auch mit dem vierten Axiom lernen wir wieder etwas Bedeutendes über die Struktur unserer Zahlenkette dazu: „Natürliche Zahlen mit gleichem Nachfolger sind gleich.“ Wenn also die Acht nach der Sieben kommt, bedeutet das, dass es keine andere Zahl gibt, nach der die Acht an der Reihe ist. Das ist wichtig, denn sonst könnte es sein, dass nach der Elf wieder die Acht kommt, die Zahlenreihe somit in sich selbst zurückgeführt wird und es außer den Zahlen von null bis elf keine weiteren Zahlen mehr gibt.

Die Zahlenkette darf also keine inneren Kreise oder Verknotungen haben, sie ist eine ordentlich aufgefädelte Reihe, in der eine Zahl auf die andere folgt. Nun wissen wir auch, dass die Kette niemals aufhört – es muss unendlich viele Zahlen geben. Das fünfte und letzte Axiom stellt noch sicher, dass die natürlichen Zahlen die kleinste Menge sind, für die diese Aussagen gelten. Damit wird ausgeschlossen, dass neben den natürlichen Zahlen, wie wir sie kennen, zusätzlich noch weitere natürliche Zahlen herumliegen, die von unserer unendlichen Zahlenkette niemals erreicht werden.

Auf diese Grundsätze können wir uns alle einigen. Und auf dieser Basis lässt sich Schritt für Schritt eine umfangreiche Zahlentheorie definieren – Addition, Multiplikation, Primzahlen. Wenn man von einer kleineren Zahl eine größere abzieht, stößt man auf eine neue Sorte von Zahlen – die negativen Zahlen. Aus ganzen Zahlen kann man Brüche bilden – die rationalen Zahlen. Das gesamte Gedankengebäude der Mathematik ist auf Basis der natürlichen Zahlen aufgebaut. Oder umgekehrt betrachtet: Die gesamte Mathematik lässt sich, wenn man ausreichend oft „Warum?“ fragt, am Ende auf die natürlichen Zahlen zurückführen, so wie man von jedem winzigen Zweig eines großen Baumes Schritt für Schritt zum Stamm gelangen kann.

Auf den ersten Blick kann man das für wissenschaftliche Liebhaberei halten, für ein hübsches, aber relativ nutzloses Spiel. Wenn wir an unserer Steuererklärung herumrechnen oder wenn wir herausfinden möchten, wie viele Fliesen wir für die Badezimmersanierung kaufen müssen, dann brauchen wir keine Axiome. Wenn wir auf dem Konto ein Minus vorfinden, ist uns ziemlich egal, wie diese seltsame negative Zahl zu Peanos Regeln passt. In all diesen Fällen befinden wir uns in dem Bereich der Mathematik, für den die meisten Leute ein ziemlich gutes Bauchgefühl haben. Und in solchen Situationen kommen wir auch ohne die logische Strenge eines klar definierten Axiomensystems zurecht.

Es gibt aber auch komplizierte Gebiete der Mathematik, in denen wir uns mit logischen Rechenregeln gewissenhaft von einer Wahrheit zur nächsten weiterarbeiten müssen, um von einer Wahrheit zur nächsten zu gelangen. Es ist so ähnlich wie beim Klettern im Gebirge: So lange die Sonne scheint, kann man ziemlich frei und unbekümmert mit Blick zum Gipfel einen Schritt nach dem anderen machen. Wenn wir uns aber in Gebiete wagen, wo uns der Nebel die freie Sicht verdeckt, dann wird es gefährlich. Dann müssen wir uns an etwas Zuverlässigem festhalten. Glück haben wir, wenn es eine Leiter gibt, die uns nach oben führt. Die Regeln einer Leiter sind einfach und klar: Wenn man die unterste Sprosse findet und weiß, wie man von einer Sprosse zur nächsten gelangt, ist es nur eine Frage der Zeit, bis man ans Ziel kommt.

Leute wie Peano zeigten: Die mathematische Logik dient nicht nur dazu, Zahlen auszurechnen und neue mathematische Wahrheiten zu finden, wir können sie auch verwenden, um die Regeln unseres Denkens genauer unter die Lupe zu nehmen. Dadurch ergaben sich für die Mathematik spannende neue Aufgaben.

In dieser Aufbruchsstimmung fand im Jahr 1900 der internationale Mathematiker-Kongress in Paris statt. Aus Göttingen, damals wohl gerade die Welthauptstadt der Mathematik, reiste der junge Professor David Hilbert an. Mit seinen achtunddreißig Jahren galt er bereits als einer der ganz Großen seines Fachs. Man erwartete von ihm eigentlich einen Rückblick, eine Zusammenfassung großer mathematischer Erfolge der Vergangenheit. Doch stattdessen beschloss Hilbert nach vorne zu schauen und dem Publikum eine Liste großer, ungelöster mathematischer Aufgaben zu präsentieren, die im neuen Jahrhundert gelöst werden sollten. Es war die größte Verteilung von Mathematik-Hausaufgaben der Wissenschaftsgeschichte.

Als die „Hilbert’schen Probleme“ ging diese Aufgabensammlung in die Geschichte ein. Und die Nummer zwei auf dieser Liste sollte die Welt der Mathematik dauerhaft verändern. Es war eine Frage, in der es um die Axiome der Mathematik ging: Lässt sich mathematisch beweisen, dass Peanos Axiome (oder ähnliche andere Konzepte) in sich widerspruchsfrei sind?

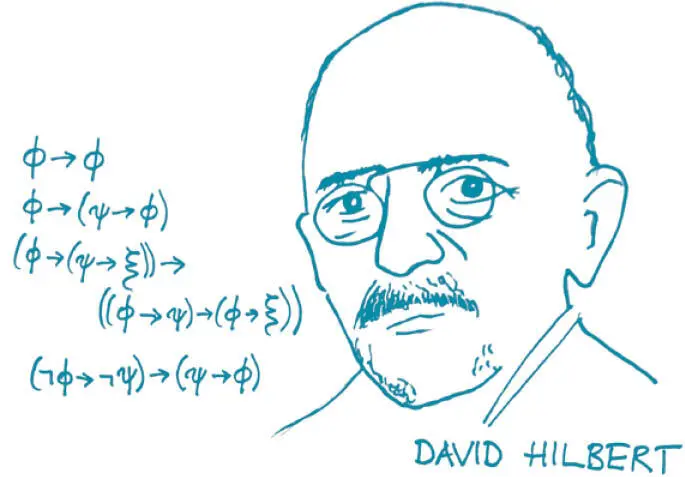
Das ist vielleicht die wichtigste Forderung, die man an die Mathematik stellen kann: Niemals darf die Mathematik zwei Aussagen zulassen, die einander widersprechen. Die beiden Sätze „A ist B“ und „A ist nicht B“ können niemals beide richtig sein, sonst würde die gesamte logische Struktur der Mathematik zusammenbrechen. Man könnte dann jede beliebige Aussage beweisen – etwa „Acht mal sieben ist vier“ oder „Deine Mutter ist ein Pinguin“.

Der große Logiker Bertrand Russell erklärte das in einer Vorlesung und wurde dann von einem Studenten gefragt: „Das heißt, unter der Annahme, dass 1=0 ist, können Sie beweisen, dass Sie der Papst sind?“ Für Russell war das kein Problem: „Wir addieren auf beiden Seiten eins – dann bekommen wir die Gleichung 2=1. Die Menge, die nur mich und den Papst enthält, hat zwei Elemente. Aber 2=1, also hat sie nur ein Element, also bin ich der Papst.“

Ist es möglich, dass aus Peanos Axiomen derart widersprüchliche Aussagen folgen? Lässt sich streng beweisen, dass ein solcher Widerspruch niemals auftreten kann? Das ist doch gar nicht nötig, könnte man vermuten. Peanos Axiome über die natürlichen Zahlen klingen doch so harmlos, so einfach und eindeutig – wie sollten sich daraus innere Widersprüche ableiten lassen? Aber solche Vermutungen sind in der Mathematik nicht genug. Ein zwingender Beweis muss her.

Dass David Hilbert einen solchen Beweis suchen wollte und dieses Projekt zu den bedeutendsten Aufgaben für die Mathematik des zwanzigsten Jahrhunderts zählte, hatte nicht zuletzt damit zu tun, dass in der Mathematik damals nicht alles so glatt und reibungslos lief, wie man sich das gewünscht hätte. Es gab einige verwirrende Probleme, über die in Mathematikerkreisen heftig gestritten wurde.

Zu den besonders komplizierten mathematischen Themen, mit denen man im neunzehnten Jahrhundert ziemlichen Ärger hatte, gehört der Begriff der Unendlichkeit. „Unendlich“ ist keine Zahl, mit der man nach den üblichen Regeln rechnen kann. Fünf ist immer fünf, und wenn das Ergebnis einer anderen Rechnung wieder fünf ist, dann ist das genau dasselbe Fünf wie vorher. Aber ist auch das Unendliche immer gleich? Gibt es unterschiedliche Arten von unendlich? Ist unendlich mal unendlich ein größeres Unendlich als unendlich plus unendlich?