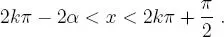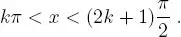Gonzalo Masjuán - Trigonometría y geometría analítica
Здесь есть возможность читать онлайн «Gonzalo Masjuán - Trigonometría y geometría analítica» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на испанском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Trigonometría y geometría analítica
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Trigonometría y geometría analítica: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Trigonometría y geometría analítica»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
integrar en un solo volumen la trigonometría, la geometría analítica, el álgebra vectorial y los números complejos, de modo que en conjunto permitan desarrollar una adecuada intuición geométrica y abordar la resolución de los diversos problemas que estas áreas consideran. La concepción pedagógica del texto permite presentar el tema como una geometría esencialmente formativa, pero también realista y utilitaria, abierta a otras áreas del conocimiento. Está dirigida a alumnos de la más diversa capacidad.


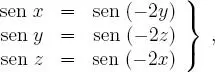
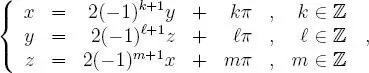
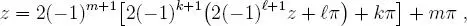
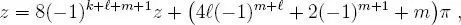
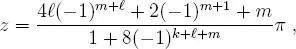
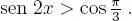
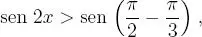
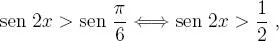
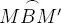 , que en particular, resulta:
, que en particular, resulta: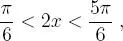
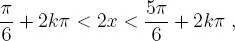
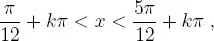
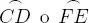 que se obtienen haciendo k = 0 y k = 1.
que se obtienen haciendo k = 0 y k = 1.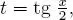 o sea:
o sea: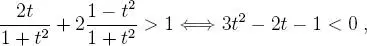
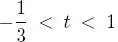 , luego,
, luego, 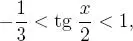 por lo tanto, los ángulos
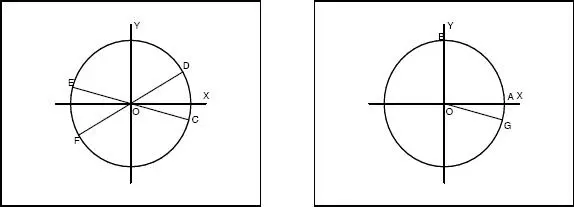
por lo tanto, los ángulos 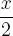 tienen su extremo en los arcos
tienen su extremo en los arcos 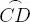 o
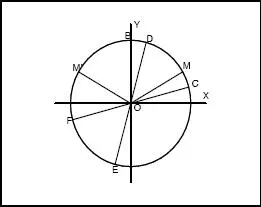
o 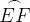 que se presentan en la figura 3.14, es decir son de la forma:
que se presentan en la figura 3.14, es decir son de la forma: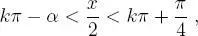
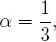 es decir α = 18 ◦26′ 5 . 82″ ≡ 0 . 321750554 radianes , con ello la solución del problema son todos aquellos ángulos cuyo lado terminal está en el arco
es decir α = 18 ◦26′ 5 . 82″ ≡ 0 . 321750554 radianes , con ello la solución del problema son todos aquellos ángulos cuyo lado terminal está en el arco 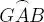 que se muestra en el segundo gráfico que aparece en la figura 8.14, es decir aquellos que cumplen con:
que se muestra en el segundo gráfico que aparece en la figura 8.14, es decir aquellos que cumplen con: